В треугольнике ABC биссектриса угла A делит высоту, проведенную из вершины B в отношении 17:15, считая от точки B. Найдите радиус окружности, описанной около треугольника ABC, если BC=16.
Рассмотрим треугольник ABF.
По свойству
биссектрисы:
BG/GF=AB/AF=17/15
cosA=AF/AB=15/17 (по
определению косинуса)
Существует тригонометрическая формула:
sin2α+cos2α=1
Тогда:
sin2∠BAF+cos2∠BAF=1
sin2∠BAF+(15/17)2=1
sin2∠BAF=1-225/289
sin2∠BAF=(289-225)/289
sin2∠BAF=64/289
sin∠BAF=8/17
По
теореме синусов:
BC/sin∠BAF=2R
16/(8/17)=16*17/8=34=2R
R=34/2=17
Ответ: R=17
Поделитесь решением
Присоединяйтесь к нам...
Какие из данных утверждений верны? Запишите их номера.
1) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
2) Площадь круга меньше квадрата длины его диаметра.
3) Если в четырёхугольнике диагонали перпендикулярны, то этот четырёхугольник — ромб.
В равнобедренную трапецию, периметр которой равен 200, а площадь равна 2000, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Длина стороны AC равна 4. Найдите радиус описанной окружности треугольника ABC.
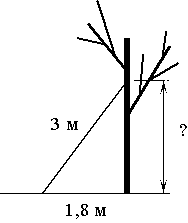Лестницу длиной 3 м прислонили к дереву. На какой высоте (в метрах) находится верхний её конец, если нижний конец отстоит от ствола дерева на 1,8 м?
Сторона ромба равна 40, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2014-05-14 20:55:14) Аделя: конечно из 2 части.