
 В треугольнике ABC на его медиане BM отмечена точка K так, что BK:KM=4:1.Прямая AK пересекает сторону BC в точке P.Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
В треугольнике ABC на его медиане BM отмечена точка K так, что BK:KM=4:1.Прямая AK пересекает сторону BC в точке P.Найдите отношение площади треугольника ABK к площади четырёхугольника KPCM.
BM -
медиана треугольника АВС,
следовательно, она делит этот треугольник на два равных по площади треугольника (
свойство медианы).
SABM=SCMB=SABC/2
Рассмотрим треугольник ABM и проведем
высоту из вершины А.
 Высота h так же является
высотой для треугольников ABK и AKM.
Высота h так же является
высотой для треугольников ABK и AKM.
Значит их площади:
SABK=h*BK*1/2
SAKM=h*KM*1/2
Найдем отношение этих площадей:
SABK/SAKM=(h*BK*1/2)/(h*KM*1/2)
SABK/SAKM=BK/KM=4
Т.е.
SAKM=SABK/4
SABK+SAKM=SABM=SABC/2
SABK+SABK/4=SABC/2
SABK*5/4=SABC/2
SABK=(SABC/2)*4/5
SABK=2*SABC/5
SAKM=SABK/4=(2*SABC/5)/4=SABC/10
Проведем отрезок CK и рассмотрим треугольники AKM и CKM.
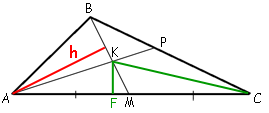 Проведем
высоту KF. Эта
высота является общей для обоих этих треугольников. Площади этих треугольников:
Проведем
высоту KF. Эта
высота является общей для обоих этих треугольников. Площади этих треугольников:
SAKM=KF*AM*1/2
SCKM=KF*CM*1/2
KF=CM (так как BM-
медиана), следовательно SAKM=SCKM=SABC/10
Тогда SCKB=SCMB-SCKM=SABC/2-SABC/10=5*SABC/10-SABC/10=4*SABC/10=2*SABC/5
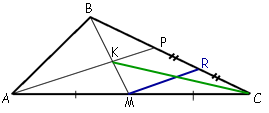 Вернемся к первоначальному рисунку и проведем отрезок MR, параллельный AP.
Вернемся к первоначальному рисунку и проведем отрезок MR, параллельный AP.
Для треугольника APC MR -
средняя линия, так как проходит через середину AC и параллельна AP.
Следовательно, по
теореме о средней линии, PR=RC.
Рассмотрим треугольники MBR и KBP.
∠MBR - общий для обоих треугольников.
∠BKP=∠BMR, так как они
соответственные (для параллельных прямых KP и MR и секущей MB).
Значит, по
первому признаку, данные треугольники
подобны.
Следовательно:
BM/BK=BR/BP
(BK+KM)/BK=(BP+PR)/BP
1+KM/BK=1+PR/BP
KM/BK=PR/BP=1/4 (по условию задачи)
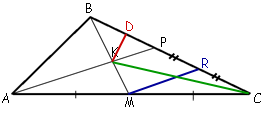 Проведем
высоту KD, как показано на рисунке.
Проведем
высоту KD, как показано на рисунке.
KD - является
высотой для треугольников KBP и KCP.
SKBP=KD*BP*1/2
SKCP=KD*CP*1/2=KD*(PR+CR)*1/2=KD*(2PR)*1/2
Найдем отношение этих площадей:
SKBP/SKCP=(KD*BP*1/2)/(KD*(2PR)*1/2)
SKBP/SKCP=BP/(2PR)=(BP/PR)/2=(4/1)/2=2
SKBP=2*SKCP
SCKB=2*SABC/5=SKBP+SKCP=2*SKCP+SKCP=3*SKCP
2*SABC/5=3*SKCP
SKCP=2*SABC/15
SKPCM = SCKM+SKCP =
SABC/10+SABC*2/15 = SABC*3/30+SABC*4/30 = SABC*7/30
SABK/SKPCM=(SABC*2/5)/(SABC*7/30)
SABK/SKPCM=(2/5)/(7/30)=(2/5)*(30/7)=(2*30)/(5*7)=(2*6)/7=12/7
Ответ: 12/7
Поделитесь решением
Присоединяйтесь к нам...
 Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Длина стороны AC равна 4. Найдите радиус описанной окружности треугольника ABC.
Медиана BM треугольника ABC является диаметром окружности, пересекающей сторону BC в её середине. Длина стороны AC равна 4. Найдите радиус описанной окружности треугольника ABC.
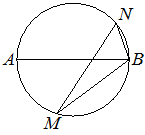 На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=69°. Найдите угол NMB. Ответ дайте в градусах.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=69°. Найдите угол NMB. Ответ дайте в градусах.
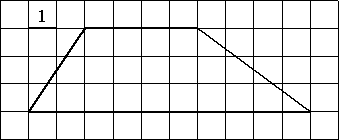 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
 В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен 75°. Найдите величину угла OAB.
В окружности с центром в точке О проведены диаметры AD и BC, угол OCD равен 75°. Найдите величину угла OAB.
 В треугольнике ABC известно, что AB=BC, ∠ABC=122°. Найдите угол BCA. Ответ дайте в градусах.
В треугольнике ABC известно, что AB=BC, ∠ABC=122°. Найдите угол BCA. Ответ дайте в градусах.
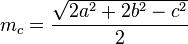 , где mc — медиана к стороне c; a, b, c — стороны треугольника. В частности, сумма квадратов медиан произвольного треугольника в 4/3 раза меньше суммы квадратов его сторон:
, где mc — медиана к стороне c; a, b, c — стороны треугольника. В частности, сумма квадратов медиан произвольного треугольника в 4/3 раза меньше суммы квадратов его сторон: 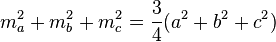
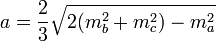 , где ma, mb, mc медианы к соответствующим сторонам треугольника, a, b, c — стороны треугольника.
, где ma, mb, mc медианы к соответствующим сторонам треугольника, a, b, c — стороны треугольника.
Комментарии:
(2015-02-09 15:58:35) Администратор: Маша, рады, что наш сайт полезен!
(2015-02-09 15:09:31) маша: Спасибо, с вами легче учиться!!!