
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ906 –Є–Ј 1087 |
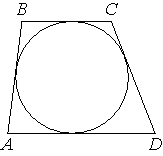 –Ґ—А–∞–њ–µ—Ж–Є—П ABCD —Б –Њ—Б–љ–Њ–≤–∞–љ–Є—П–Љ–Є AD –Є BC –Њ–њ–Є—Б–∞–љ–∞ –Њ–Ї–Њ–ї–Њ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, AB=14, BC=13, CD=22. –Э–∞–є–і–Є—В–µ AD.
–Ґ—А–∞–њ–µ—Ж–Є—П ABCD —Б –Њ—Б–љ–Њ–≤–∞–љ–Є—П–Љ–Є AD –Є BC –Њ–њ–Є—Б–∞–љ–∞ –Њ–Ї–Њ–ї–Њ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, AB=14, BC=13, CD=22. –Э–∞–є–і–Є—В–µ AD.
–Ґ–∞–Ї –Ї–∞–Ї –≤ —В—А–∞–њ–µ—Ж–Є—О –≤–њ–Є—Б–∞–љ–∞
–Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М, —В–Њ:
AD+BC=A–Т+CD (–њ–Њ —З–µ—В–≤–µ—А—В–Њ–Љ—Г —Б–≤–Њ–є—Б—В–≤—Г —В—А–∞–њ–µ—Ж–Є–Є).
AD+13=14+22
AD=14+22-13=23
–Ю—В–≤–µ—В: 23
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
 –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —Г–≥–Њ–ї C –њ—А—П–Љ–Њ–є, BC=6, sinA=0,6. –Э–∞–є–і–Є—В–µ AB.
–Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —Г–≥–Њ–ї C –њ—А—П–Љ–Њ–є, BC=6, sinA=0,6. –Э–∞–є–і–Є—В–µ AB.
–£–Ї–∞–ґ–Є—В–µ –љ–Њ–Љ–µ—А–∞ –≤–µ—А–љ—Л—Е —Г—В–≤–µ—А–ґ–і–µ–љ–Є–є.
1) –¶–µ–љ—В—А –≤–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —А–∞–≤–љ–Њ–±–µ–і—А–µ–љ–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –ї–µ–ґ–Є—В –љ–∞ –≤—Л—Б–Њ—В–µ, –њ—А–Њ–≤–µ–і—С–љ–љ–Њ–є –Ї –Њ—Б–љ–Њ–≤–∞–љ–Є—О —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞.
2) –†–Њ–Љ–± –љ–µ —П–≤–ї—П–µ—В—Б—П –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–Њ–Љ.
3) –°—Г–Љ–Љ–∞ –Њ—Б—В—А—Л—Е —Г–≥–ї–Њ–≤ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ–∞ 90¬∞.
 –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —Г–≥–Њ–ї C —А–∞–≤–µ–љ 90¬∞, sinB=3/7, AB=21. –Э–∞–є–і–Є—В–µ AC.
–Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC —Г–≥–Њ–ї C —А–∞–≤–µ–љ 90¬∞, sinB=3/7, AB=21. –Э–∞–є–і–Є—В–µ AC.
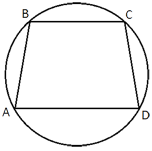 –Ю–Ї–Њ–ї–Њ —В—А–∞–њ–µ—Ж–Є–Є, –Њ–і–Є–љ –Є–Ј —Г–≥–ї–Њ–≤ –Ї–Њ—В–Њ—А–Њ–є —А–∞–≤–µ–љ 49¬∞, –Њ–њ–Є—Б–∞–љ–∞ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М. –Э–∞–є–і–Є—В–µ –Њ—Б—В–∞–ї—М–љ—Л–µ —Г–≥–ї—Л —В—А–∞–њ–µ—Ж–Є–Є.
–Ю–Ї–Њ–ї–Њ —В—А–∞–њ–µ—Ж–Є–Є, –Њ–і–Є–љ –Є–Ј —Г–≥–ї–Њ–≤ –Ї–Њ—В–Њ—А–Њ–є —А–∞–≤–µ–љ 49¬∞, –Њ–њ–Є—Б–∞–љ–∞ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М. –Э–∞–є–і–Є—В–µ –Њ—Б—В–∞–ї—М–љ—Л–µ —Г–≥–ї—Л —В—А–∞–њ–µ—Ж–Є–Є.
 –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC –Є–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ AB=BC, ∠ABC=102¬∞. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї BCA. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC –Є–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ AB=BC, ∠ABC=102¬∞. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї BCA. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
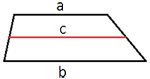
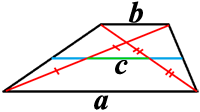
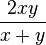 (—Б—А–µ–і–љ–µ–µ –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Њ–µ), –≥–і–µ x –Є y вАФ –Њ—Б–љ–Њ–≤–∞–љ–Є—П —В—А–∞–њ–µ—Ж–Є–Є (—Д–Њ—А–Љ—Г–ї–∞ –С—Г—А–∞–Ї–Њ–≤–∞).
(—Б—А–µ–і–љ–µ–µ –≥–∞—А–Љ–Њ–љ–Є—З–µ—Б–Ї–Њ–µ), –≥–і–µ x –Є y вАФ –Њ—Б–љ–Њ–≤–∞–љ–Є—П —В—А–∞–њ–µ—Ж–Є–Є (—Д–Њ—А–Љ—Г–ї–∞ –С—Г—А–∞–Ї–Њ–≤–∞).
–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є:
(2019-12-25 08:18:36) –°.: —В—А–∞–њ–µ—Ж–Є—П –∞–±—Б–і —Б –Њ—Б–љ–Њ–≤–∞–љ–Є—П–Љ–Є –∞–і –Є –±—Б –≤–њ–Є—Б–∞–љ–∞ –≤ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М. —В–∞–Ї,—З—В–Њ –∞–і-–і–Є–∞–Љ–µ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є .–Ф–Є–∞–≥–Њ–љ–∞–ї—М —В—А–∞–њ–µ—Ж–Є–Є —А–∞–≤–љ–∞ 10 —Б–Љ,–∞ –µ—С –њ–ї–Њ—Й–∞–і—М - 25—Б–Љ2.