ОГЭ, Математика.
Геометрия: Задача №466413

Задача №969 из 1087
Условие задачи:

Радиус окружности, описанной около квадрата, равен 36√2. Найдите длину стороны этого квадрата.

Решение задачи:

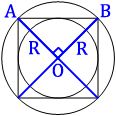Проведем диаметры описанной окружности, как показано на первом рисунке.
Очевидно, что квадрат разделился на 4 равных треугольника, углы, которые опираются на центр окружности (О), равны 360°/4=90°, т.е. эти треугольники прямоугольные.
Тогда, по теореме Пифагора:
AB²=R²+R²
AB²=2R²
AB²=2(36√2)²
AB²=2*36²*2
AB²=36²*2²=(36*2)²=72²
AB=72
Ответ: 72

Поделитесь решением

Присоединяйтесь к нам...

Вы можете поблагодарить автора, написать свои претензии или предложения на странице 'Про нас'

Другие задачи из этого раздела

Задача №58CE70

Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой накрест лежащие углы равны, то прямые параллельны.
2) Диагональ трапеции делит её на два равных треугольника.
3) Квадрат диагонали прямоугольника равен сумме квадратов двух его смежных сторон.

Задача №310EA3

Проектор полностью освещает экран A высотой 190 см, расположенный на расстоянии 210 см от проектора. Найдите, на каком наименьшем расстоянии от проектора нужно расположить экран B высотой 380 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными. Ответ дайте в сантиметрах.