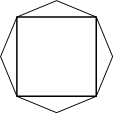
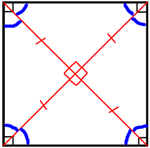
Дан правильный восьмиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится квадрат.
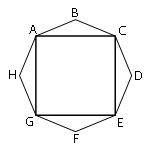Рассмотрим треугольники ABC, CDE, EFG и GHA. AB=BC=CD=DE=EF=FG=GH=HA (по
определению правильного многоугольника).
/ABC=/CDE=/EFG=/GHA (по
определению правильного многоугольника).
Следовательно, рассматриваемые треугольники равны (по
первому признаку равенства треугольников).
Это означает, что AC=CE=EG=GA.
Из равенства этих треугольников также следует, что все их острые углы тоже равны (/BAC=/BCA=/DCE=...и т.д.). Следовательно, /ACE=/CEG=/EGA=/GAC.
В итоге, по
определению правильного многоугольника получается, что ACEG - правильный многоугольник. А т.к. этот многоугольник имеет 4 угла, то это
квадрат.
Поделитесь решением
Присоединяйтесь к нам...
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 5,25, а AB=9.
В равнобедренную трапецию, периметр которой равен 180, а площадь равна 1620, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.
В окружности с центром в точке О проведены диаметры AD и BC, угол
OAB равен 80°. Найдите величину угла OCD.
На стороне АС треугольника АВС выбраны точки D и E так, что отрезки AD и CE равны (см. рисунок). Оказалось, что углы АDB и BEC тоже равны. Докажите, что треугольник АВС — равнобедренный.
В треугольнике ABC DE – средняя линия. Площадь треугольника CDE равна 35. Найдите площадь треугольника ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: