Центр окружности, описанной около треугольника ABC, лежит на стороне AB. Радиус окружности равен 10. Найдите BC, если AC=16.
По
теореме об описанной окружности, центр описанной окружности лежит на точке пересечения
серединных перпендикуляров сторон треугольника.
У
прямоугольного треугольника центр окрудности лежит на середине гипотенузы, так же как и в треугольнике нашей задачи, следовательно данный треугольник
прямоугольный.
Следовательно, можно применить
теорему Пифагора:
AB2=BC2+AC2
AB - диаметр окружности, так как проходит через центр.
Тогда AB=2*R=2*10=20.
202=BC2+162
400=BC2+256
BC2=400-256=144
BC=12
Ответ: 12
Поделитесь решением
Присоединяйтесь к нам...
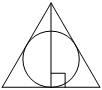Радиус окружности, вписанной в равносторонний треугольник, равен 5. Найдите высоту этого треугольника.
В треугольнике ABC угол C равен 90°, AC=12 , tgA=2√
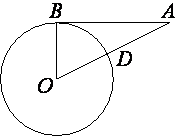Отрезок AB=32 касается окружности радиуса 24 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
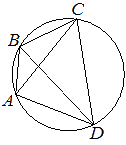Четырёхугольник ABCD вписан в окружность. Угол ABC равен 138°, угол CAD равен 83°. Найдите угол ABD. Ответ дайте в градусах.
Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите PK, если BH=16.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: