В треугольнике ABC AC=35, BC=5√
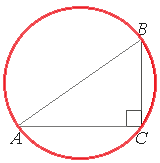Треугольник ABC -
прямоугольный, тогда по
теореме Пифагора:
AB2=AC2+BC2
AB2=352+(5√
AB2=1225+25*15
AB2=1600
AB=40
Так как треугольник ABC прямоугольный, то это означает, что центр окружности находится на середине гипотенузы (по
теореме об описанной окружности).
Тогда R=AB/2=40/2=20
Ответ: R=20
Поделитесь решением
Присоединяйтесь к нам...
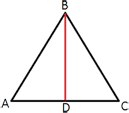Сторона равностороннего треугольника равна 10√
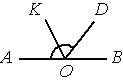Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB=52°. Ответ дайте в градусах.
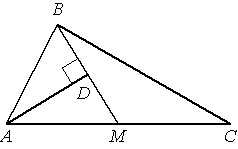Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АВ, если сторона АС равна 10.
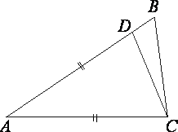Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=80° и ∠ACB=59°. Найдите угол DCB. Ответ дайте в градусах.
В треугольнике два угла равны 72° и 42°. Найдите его третий угол. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: