Основания трапеции равны 3 и 9, а высота равна 5. Найдите среднюю линию этой трапеции.
Средняя линия трапеции равна полусумме оснований и не зависит от высоты:
m=(3+9)/2=12/2=6
Ответ: 6
Поделитесь решением
Присоединяйтесь к нам...
Сторона AB параллелограмма ABCD вдвое больше стороны AD. Точка K — середина стороны AB. Докажите, что DK — биссектриса угла ADC.
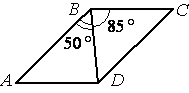Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
50° и 85°. Найдите меньший угол параллелограмма.
Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АС, если сторона АВ равна 4.
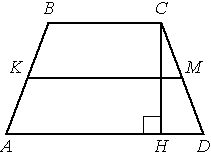В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 6.
Радиус вписанной в квадрат окружности равен 22√2. Найдите диагональ этого квадрата.
Хочу получать новые решения
Ни какого спама
, или 
, где m - средняя линия трапеции. 
Автор: Таська
Комментарии: