
 Площадь параллелограмма ABCD равна 176. Точка E — середина стороны AD. Найдите площадь трапеции AECB.
Площадь параллелограмма ABCD равна 176. Точка E — середина стороны AD. Найдите площадь трапеции AECB.
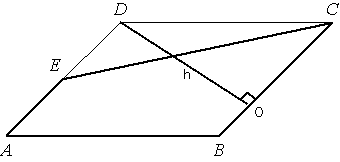 Проведем высоту
параллелограмма DO, как показано на рисунке. Площадь параллелограмма равна произведению стороны на высоту
параллелограмма.
Проведем высоту
параллелограмма DO, как показано на рисунке. Площадь параллелограмма равна произведению стороны на высоту
параллелограмма.
Sпараллелограмма=BC*h=176
А площадь
трапеции равна произведению полусуммы оснований на высоту.
Sтрапеции=h*(BC+AE)/2.
AE=AD/2 (по условию задачи).
AD=BC (по
свойству параллелограмма).
Следовательно AE=BC/2.
Тогда Sтрапеции=h*(BC+BC/2)/2 = h*(3*BC/2)/2 = h*3*BC/4=h*BC*3/4 = Sпарал-ма*3/4=176*3/4=132.
Ответ: 132
Поделитесь решением
Присоединяйтесь к нам...
Основание AC равнобедренного треугольника ABC равно 4. Окружность радиуса 2,5 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
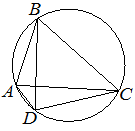 Четырёхугольник ABCD вписан в окружность. Угол ABC равен 70°, угол CAD равен 49°. Найдите угол ABD. Ответ дайте в градусах.
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 70°, угол CAD равен 49°. Найдите угол ABD. Ответ дайте в градусах.
 Высота AH ромба ABCD делит сторону CD на отрезки DH=8 и CH=2. Найдите высоту ромба.
Высота AH ромба ABCD делит сторону CD на отрезки DH=8 и CH=2. Найдите высоту ромба.
 Сторона равностороннего треугольника равна 2√
Сторона равностороннего треугольника равна 2√
 Площадь прямоугольного треугольника равна 882√
Площадь прямоугольного треугольника равна 882√

 , или
, или  , где m - средняя линия трапеции.
, где m - средняя линия трапеции.
Комментарии: