В трапеции ABCD AB=CD, ∠BDA=49° и ∠BDC=13°. Найдите угол ABD. Ответ дайте в градусах.
∠ADC=∠BDA+∠BDC=49°+13°=62°.
Трапеция ABCD -
равнобедренная (т.к. AB=CD), следовательно, по
свойству равнобедренной трапеции, ∠BAD=∠ADC=62°.
Рассмотрим треугольник ABD:
По
теореме о сумме углов треугольника:
180°=∠BAD+∠ABD+∠BDA
180°=62°+∠ABD+49°
∠ABD=180°-62°-49°
∠ABD=69°
Ответ: 69
Поделитесь решением
Присоединяйтесь к нам...
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=24, BF=32.
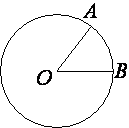На окружности с центром O отмечены точки A и B так, что
/AOB=66°. Длина меньшей дуги AB равна 99. Найдите длину большей дуги.
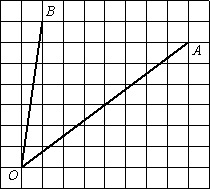Найдите тангенс угла AOB.
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB=15, AC=25.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 60° и 150°, а CD=33.
Хочу получать новые решения
Ни какого спама
, или 
, где m - средняя линия трапеции. 
Автор: Таська
Комментарии: