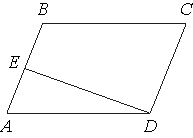
Площадь параллелограмма ABCD равна 6. Точка E – середина стороны AB. Найдите площадь трапеции EBCD.
Вариант №1
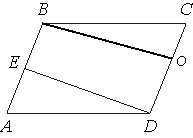Проведем высоту
параллелограмма BO, как показано на рисунке. Площадь параллелограмма равна произведению стороны на высоту
параллелограмма.
Sпараллелограмма=CD*h=6
А площадь
трапеции равна произведению полусуммы оснований на высоту.
Sтрапеции=h*(EB+CD)/2.
EB=AB/2 (по условию задачи).
AB=CD (по
свойству параллелограмма).
Следовательно EB=CD/2.
Тогда Sтрапеции=h*(CD/2+CD)/2 = h*(3*CD/2)/2 = h*3*CD/4=h*CD*3/4 = Sпарал-ма*3/4=6*3/4=4,5.
Ответ: 4,5
Проведем отрезки как показано на рисунке.Поделитесь решением
Присоединяйтесь к нам...
Хорды AC и BD окружности пересекаются в точке P, BP=9, CP=15, DP=20. Найдите AP.
Диагональ прямоугольника образует угол 75° с одной из его сторон. Найдите угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
Радиус окружности, описанной около квадрата, равен 48√2. Найдите радиус окружности, вписанной в этот квадрат.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 136. Найдите стороны треугольника ABC.
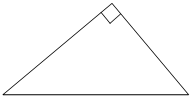В прямоугольном треугольнике катет и гипотенуза равны 16 и 20 соответственно. Найдите другой катет этого треугольника.
Хочу получать новые решения
Ни какого спама
, или 
, где m - средняя линия трапеции. 
Автор: Таська
Комментарии:
(2017-05-28 22:46:35) Администратор: Alissa, отличное решение, спасибо!
(2017-05-20 12:39:40) Alissa: Можно доказать, что площадь параллелограмма состоит из 4х равновеликих треугольников. Поэтому, площадь треугольника ADE составляет 1/4 площади параллелограмма. Тогда площадь трапеции ЕВСD составляет 3/4 площади параллелограмма .S=3/4*6=4,5 .Ответ:4,5
(2017-03-04 11:23:10) Ляля: Спасибо,всё очень понятно и просто!