
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ467 –Є–Ј 1087 |
 –Т —В—А–∞–њ–µ—Ж–Є–Є ABCD AD=4, BC=1, –∞ –µ—С –њ–ї–Њ—Й–∞–і—М —А–∞–≤–љ–∞ 35. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC.
–Т —В—А–∞–њ–µ—Ж–Є–Є ABCD AD=4, BC=1, –∞ –µ—С –њ–ї–Њ—Й–∞–і—М —А–∞–≤–љ–∞ 35. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC.
–Я–ї–Њ—Й–∞–і—М
—В—А–∞–њ–µ—Ж–Є–Є —А–∞–≤–љ–∞ h*(a+b)/2, –≥–і–µ a –Є b - –Њ—Б–љ–Њ–≤–∞–љ–Є—П —В—А–∞–њ–µ—Ж–Є–Є, h - –≤—Л—Б–Њ—В–∞ —В—А–∞–њ–µ—Ж–Є–Є.
h—В—А–∞–њ–µ—Ж–Є–Є*(4+1)/2=35 (–њ–Њ —Г—Б–ї–Њ–≤–Є—О –Ј–∞–і–∞—З–Є)
h=35/2,5=14
 –Я—А–Њ–≤–µ–і–µ–Љ
–≤—Л—Б–Њ—В—Г —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC, –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞–љ–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
–Я—А–Њ–≤–µ–і–µ–Љ
–≤—Л—Б–Њ—В—Г —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC, –Ї–∞–Ї –њ–Њ–Ї–∞–Ј–∞–љ–Њ –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
h—В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞=h—В—А–∞–њ–µ—Ж–Є–Є, —В–∞–Ї –Ї–∞–Ї –Њ–љ–Є –Њ–±–µ –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ—Л –Њ–і–љ–Є–Љ –Є —В–µ–Љ –ґ–µ –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л–Љ –Њ—Б–љ–Њ–≤–∞–љ–Є—П–Љ —В—А–∞–њ–µ—Ж–Є–Є –Є –Њ–±—А–∞–Ј—Г—О—В –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї.
S—В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞=h—В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞*BC/2=14*1/2=7
–Ю—В–≤–µ—В: S—В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞=7
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
 –Т –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —Б —Ж–µ–љ—В—А–Њ–Љ –≤ —В–Њ—З–Ї–µ –Ю –њ—А–Њ–≤–µ–і–µ–љ—Л –і–Є–∞–Љ–µ—В—А—Л AD –Є BC, —Г–≥–Њ–ї
OCD —А–∞–≤–µ–љ 80¬∞. –Э–∞–є–і–Є—В–µ –≤–µ–ї–Є—З–Є–љ—Г —Г–≥–ї–∞ OAB.
–Т –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —Б —Ж–µ–љ—В—А–Њ–Љ –≤ —В–Њ—З–Ї–µ –Ю –њ—А–Њ–≤–µ–і–µ–љ—Л –і–Є–∞–Љ–µ—В—А—Л AD –Є BC, —Г–≥–Њ–ї
OCD —А–∞–≤–µ–љ 80¬∞. –Э–∞–є–і–Є—В–µ –≤–µ–ї–Є—З–Є–љ—Г —Г–≥–ї–∞ OAB.
 –Э–∞ –Ї–∞–Ї–Њ–Љ —А–∞—Б—Б—В–Њ—П–љ–Є–Є (–≤ –Љ–µ—В—А–∞—Е) –Њ—В —Д–Њ–љ–∞—А—П —Б—В–Њ–Є—В —З–µ–ї–Њ–≤–µ–Ї —А–Њ—Б—В–Њ–Љ 1,8 –Љ, –µ—Б–ї–Є –і–ї–Є–љ–∞ –µ–≥–Њ —В–µ–љ–Є —А–∞–≤–љ–∞ 9 –Љ, –≤—Л—Б–Њ—В–∞ —Д–Њ–љ–∞—А—П 4 –Љ?
–Э–∞ –Ї–∞–Ї–Њ–Љ —А–∞—Б—Б—В–Њ—П–љ–Є–Є (–≤ –Љ–µ—В—А–∞—Е) –Њ—В —Д–Њ–љ–∞—А—П —Б—В–Њ–Є—В —З–µ–ї–Њ–≤–µ–Ї —А–Њ—Б—В–Њ–Љ 1,8 –Љ, –µ—Б–ї–Є –і–ї–Є–љ–∞ –µ–≥–Њ —В–µ–љ–Є —А–∞–≤–љ–∞ 9 –Љ, –≤—Л—Б–Њ—В–∞ —Д–Њ–љ–∞—А—П 4 –Љ?
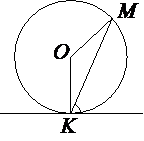 –Я—А—П–Љ–∞—П –Ї–∞—Б–∞–µ—В—Б—П –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є –≤ —В–Њ—З–Ї–µ K. –Ґ–Њ—З–Ї–∞ O вАУ —Ж–µ–љ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є. –•–Њ—А–і–∞ KM –Њ–±—А–∞–Ј—Г–µ—В —Б –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є —Г–≥–Њ–ї, —А–∞–≤–љ—Л–є 83¬∞. –Э–∞–є–і–Є—В–µ –≤–µ–ї–Є—З–Є–љ—Г —Г–≥–ї–∞ OMK. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–Я—А—П–Љ–∞—П –Ї–∞—Б–∞–µ—В—Б—П –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є –≤ —В–Њ—З–Ї–µ K. –Ґ–Њ—З–Ї–∞ O вАУ —Ж–µ–љ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є. –•–Њ—А–і–∞ KM –Њ–±—А–∞–Ј—Г–µ—В —Б –Ї–∞—Б–∞—В–µ–ї—М–љ–Њ–є —Г–≥–Њ–ї, —А–∞–≤–љ—Л–є 83¬∞. –Э–∞–є–і–Є—В–µ –≤–µ–ї–Є—З–Є–љ—Г —Г–≥–ї–∞ OMK. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
 –Т –≤—Л–њ—Г–Ї–ї–Њ–Љ —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–µ NPQM –і–Є–∞–≥–Њ–љ–∞–ї—М NQ —П–≤–ї—П–µ—В—Б—П –±–Є—Б—Б–µ–Ї—В—А–Є—Б–Њ–є —Г–≥–ї–∞ PNM –Є –њ–µ—А–µ—Б–µ–Ї–∞–µ—В—Б—П —Б –і–Є–∞–≥–Њ–љ–∞–ї—М—О PM –≤ —В–Њ—З–Ї–µ S. –Э–∞–є–і–Є—В–µ NS, –µ—Б–ї–Є –Є–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ –Њ–Ї–Њ–ї–Њ —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–∞ NPQM –Љ–Њ–ґ–љ–Њ –Њ–њ–Є—Б–∞—В—М –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М, PQ=86, SQ=43.
–Т –≤—Л–њ—Г–Ї–ї–Њ–Љ —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–µ NPQM –і–Є–∞–≥–Њ–љ–∞–ї—М NQ —П–≤–ї—П–µ—В—Б—П –±–Є—Б—Б–µ–Ї—В—А–Є—Б–Њ–є —Г–≥–ї–∞ PNM –Є –њ–µ—А–µ—Б–µ–Ї–∞–µ—В—Б—П —Б –і–Є–∞–≥–Њ–љ–∞–ї—М—О PM –≤ —В–Њ—З–Ї–µ S. –Э–∞–є–і–Є—В–µ NS, –µ—Б–ї–Є –Є–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ –Њ–Ї–Њ–ї–Њ —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–∞ NPQM –Љ–Њ–ґ–љ–Њ –Њ–њ–Є—Б–∞—В—М –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М, PQ=86, SQ=43.
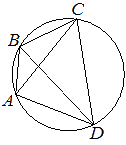 –І–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї ABCD –≤–њ–Є—Б–∞–љ –≤ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М. –£–≥–Њ–ї ABC —А–∞–≤–µ–љ 138¬∞, —Г–≥–Њ–ї CAD —А–∞–≤–µ–љ 83¬∞. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї ABD. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–І–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї ABCD –≤–њ–Є—Б–∞–љ –≤ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М. –£–≥–Њ–ї ABC —А–∞–≤–µ–љ 138¬∞, —Г–≥–Њ–ї CAD —А–∞–≤–µ–љ 83¬∞. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї ABD. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.

 , –Є–ї–Є
, –Є–ї–Є  , –≥–і–µ m - —Б—А–µ–і–љ—П—П –ї–Є–љ–Є—П —В—А–∞–њ–µ—Ж–Є–Є.
, –≥–і–µ m - —Б—А–µ–і–љ—П—П –ї–Є–љ–Є—П —В—А–∞–њ–µ—Ж–Є–Є.
–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є:
(2016-10-18 14:36:11) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –љ–∞—Б—В—П, –Ь—Л –љ–µ –њ–Њ–Љ–Њ–≥–∞–µ–Љ —А–µ—И–Є—В—М –і–Њ–Љ–∞—И–љ–µ–µ –Ј–∞–і–∞–љ–Є–µ, —Ж–µ–ї—М —Б–∞–є—В–∞ - –њ–Њ–і—А–Њ–±–љ–Њ —А–∞–Ј–Њ–±—А–∞—В—М –Ј–∞–і–∞—З–Є, –Ї–Њ—В–Њ—А—Л–µ –±—Г–і—Г—В –љ–∞ —Н–Ї–Ј–∞–Љ–µ–љ–∞—Е, —З—В–Њ–±—Л —Г—З–∞—Й–Є–µ—Б—П –љ–∞—Г—З–Є–ї–Є—Б—М –Є—Е —А–µ—И–∞—В—М —Б–∞–Љ–Њ—Б—В–Њ—П—В–µ–ї—М–љ–Њ. –Х—Б–ї–Є –љ–∞–є–і–µ—В–µ –њ–Њ—Е–Њ–ґ—Г—О –Ј–∞–і–∞—З—Г –љ–∞ —Б–∞–є—В–µ fipi.ru, –њ–Є—И–Є—В–µ, –Њ–±—П–Ј–∞—В–µ–ї—М–љ–Њ –і–Њ–±–∞–≤–Є–Љ.
(2016-10-18 14:27:06) –љ–∞—Б—В—П: –і–∞–љ–Њ –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–∞—П —В—А–∞–њ–µ—Ж–Є—П –∞–≤—Бd –∞d=4 –Ф–Ы–Ш–Э–Р –Т–°=2 –£–У–Ю–Ы D=45 –У–†–Р–Ф–£–°–Ю–Т –Э–Р–Щ–Ґ–Ш –Я–†–Ю–Х–Ъ–¶–Ш–Ш –Т–Х–Ъ–Ґ–Ю–†–Ю–Т –РD AB BC AC –Э–Р –Т–Х–Ъ–Ґ–Ю–† CD
(2014-05-26 13:31:53) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Ъ–Њ–ї—П, –≤—Л—Б–Њ—В–∞ –Њ–±—Й–∞—П. –Я—А–Њ—Б—В–Њ –љ–µ –≤—Б–µ–Љ –њ–Њ–ї—М–Ј–Њ–≤–∞—В–µ–ї—П–Љ —Н—В–Њ —Б—А–∞–Ј—Г –њ–Њ–љ—П—В–љ–Њ, –њ–Њ—Н—В–Њ–Љ—Г –≤ —А–µ—И–µ–љ–Є–Є —Н—В–Њ –і–Њ–Ї–∞–Ј—Л–≤–∞–µ—В—Б—П.
(2014-05-26 10:41:11) –Ъ–Њ–ї—П : –Р —А–∞–Ј–≤–µ –≤—Л—Б–Њ—В–∞ h—В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –љ–µ –±—Г–і–µ—В –Њ–±—Й–µ–є –≤—Л—Б–Њ—В–Њ–є –Є –і–ї—П —В—А–∞–њ–µ—Ж–Є–Є ?
(2014-05-25 12:50:54) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Ґ–∞–љ—О—И–Ї–∞, –Љ–Њ–ґ–љ–Њ –Є —В–∞–Ї.
(2014-05-25 11:56:49) —В–∞–љ—О—И–Ї–∞: –Ь–Њ–ґ–љ–Њ —А–µ—И–Є—В—М –і—А—Г–≥–Є–Љ —Б–њ–Њ—Б–Њ–±–Њ–Љ. –Э–∞—Е–Њ–і–Є–Љ —В–∞–Ї–ґ–µ –≤—Л—Б–Њ—В—Г —В—А–∞–њ–µ—Ж–Є–Є. –Ю–љ–∞ —А–∞–≤–љ–∞ 14. –≠—В–∞ –ґ–µ –≤—Л—Б–Њ—В–∞ —П–≤–ї—П–µ—В—Б—П –≤—Л—Б–Њ—В–Њ–є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –Р–°D. –Э–∞—Е–Њ–і–Є–Љ –µ–≥–Њ –њ–ї–Њ—Й–∞–і—М=AD*H/2=4*14/2=28. –Ґ–µ–њ–µ—А—М –љ–∞—Е–Њ–і–Є–Љ –њ–ї–Њ—Й–∞–і—М —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC=35-28=7
(2014-05-19 16:48:07) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Ы–Є–Ј–∞, –Њ–±–µ –≤—Л—Б–Њ—В—Л (–Є —В—А–∞–њ–µ—Ж–Є–Є, –Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞) –њ–µ—А–њ–µ–љ–і–Є–Ї—Г–ї—П—А–љ—Л –Њ—Б–љ–Њ–≤–∞–љ–Є—П–Љ —В—А–∞–њ–µ—Ж–Є–Є, –Ї–Њ—В–Њ—А—Л–µ –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л –і—А—Г–≥ –і—А—Г–≥—Г. –Ґ–∞–Ї–Є–Љ –Њ–±—А–∞–Ј–Њ–Љ, –≤—Л—Б–Њ—В—Л —П–≤–ї—П—О—В—Б—П –њ—А–Њ—В–Є–≤–Њ–њ–Њ–ї–Њ–ґ–љ—Л–Љ–Є —Б—В–Њ—А–Њ–љ–∞–Љ–Є –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Є–Ї–∞, –њ–Њ—Н—В–Њ–Љ—Г –Њ–љ–Є —А–∞–≤–љ—Л. –Ф–∞ –Њ–љ–Є –Є –љ–µ –Љ–Њ–≥—Г—В –±—Л—В—М —А–∞–Ј–љ—Л–Љ–Є. –Э–∞–≤–µ—А–љ–Њ, –≤—Л –љ–µ –њ—А–∞–≤–Є–ї—М–љ–Њ –њ—А–Њ—З–Є—В–∞–ї–Є —А–Є—Б—Г–љ–Њ–Ї.
(2014-05-19 15:31:04) –Ы–Є–Ј–∞: –Т—Л—Б–Њ—В—Л –љ–µ –Љ–Њ–≥—Г –±—Л—В—М —А–∞–≤–љ—Л! –Ф–∞–ґ–µ –µ—Б–ї–Є –њ–Њ —А–Є—Б—Г–љ–Ї—Г –њ–Њ—Б–Љ–Њ—В—А–µ—В—М, —В–Њ –≤—Л—Б–Њ—В–∞ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –≤ 2 —А–∞–Ј–∞ –Љ–µ–љ—М—И–µ –≤—Л—Б–Њ—В—Л —В—А–∞–њ–µ—Ж–Є–Є, —В–Ї –≤—Л—Б–Њ—В–∞ —В—А–∞–њ–µ—Ж–Є–Є –њ–µ—А–µ—Б–µ–Ї–∞–µ—В —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї —В–∞–Љ, –≥–і–µ –љ–∞—Е–Њ–і–Є—В—Б—П —Б—А–µ–і–љ—П—П –ї–Є–љ–Є—П