В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 8. Найдите площадь четырёхугольника ABMN.
MN -
средняя линия треугольника ABC, по теореме о средней линии NM=AB/2 => 2NM=AB.
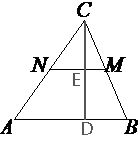Проведем
высоту из вершины С.
SCNM=1/2*CE*NM=8 (по условию).
CE*NM=16
Рассмотрим треугольник ACD, NE||AD и идет из середины стороны AC, следовательно NE -
средняя линия для треугольника ACD, значит CE=ED.
ABMN - трапеция (по
определению), тогда
SABMN=(NM+AB)/2*ED. Подставляем ранее выявленные равенства, получаем:
SABMN=(NM+2NM)/2*CE=3NM/2*CE=1,5NM*CE=1,5*16=24
Ответ: SABMN=24
Поделитесь решением
Присоединяйтесь к нам...
Проектор полностью освещает экран A высотой 80 см, расположенный на расстоянии 250 см от проектора. На каком наименьшем расстоянии
(в сантиметрах) от проектора нужно расположить экран B высотой 160 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно. Найдите BN, если MN=17, AC=51, NC=32.
Периметр треугольника равен 33, одна из сторон равна 7,
а радиус вписанной в него окружности равен 2. Найдите площадь этого треугольника.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что /NBA=11°. Найдите угол NMB. Ответ дайте в градусах.
Центральный угол AOB опирается на хорду АВ длиной 6. При этом угол ОАВ равен 60°. Найдите радиус окружности.
Хочу получать новые решения
Ни какого спама
, или 
, где m - средняя линия трапеции. 
Автор: Таська
Комментарии: