
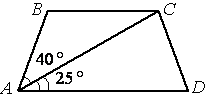 Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 25° и 40° соответственно.
Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 25° и 40° соответственно.
По свойству
равнобедренной трапеции - углы при основании равны. Тогда /CDA=/BAD=40°+25°=65°.
AD||BC (по
определению трапеции), тогда сторону AB можно рассматривать как секущую к этим параллельным прямым.
Следовательно, /DAB+/ABC=180° (т.к. эти углы
внутренние односторонние) => /ABC=180°-/DAB=180°-65°=115°.
/BCD=/DAB=115° (по
свойству равнобедренной трапеции).
Следовательно, это и есть бОльшие углы трапеции.
Ответ: больший угол трапеции = 115°.
Поделитесь решением
Присоединяйтесь к нам...
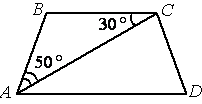 Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные
30° и 50° соответственно.
Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные
30° и 50° соответственно.
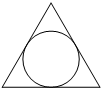 Радиус окружности, вписанной в равносторонний треугольник, равен 2√
Радиус окружности, вписанной в равносторонний треугольник, равен 2√
 Радиус вписанной в квадрат окружности равен 7√
Радиус вписанной в квадрат окружности равен 7√
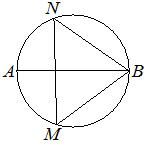 На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=36°. Найдите угол NMB. Ответ дайте в градусах.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=36°. Найдите угол NMB. Ответ дайте в градусах.
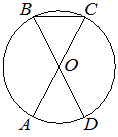 В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 50°. Найдите угол ACB. Ответ дайте в градусах.
В окружности с центром в точке O отрезки AC и BD — диаметры. Угол AOD равен 50°. Найдите угол ACB. Ответ дайте в градусах.

 , или
, или  , где m - средняя линия трапеции.
, где m - средняя линия трапеции.
Комментарии: