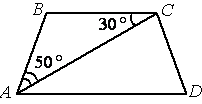Найдите угол АDС равнобедренной трапеции ABCD, если диагональ АС образует с основанием ВС и боковой стороной АВ углы, равные
30° и 50° соответственно.
В треугольнике ABC угол /ABC=180°-/BAC-/BCA=180°-50°-30°=100° (по
теореме о сумме углов треугольника).
Любую
равнобедренную трапецию можно вписать в окружность (
свойство описанной окружности), следовательно, сумма противоположных углов трапеции равна 180° по
третьему свойству описанной окружности. Следовательно, /ABC+/ADC=180°
/ADC=180°-100°=80°.
Ответ: /ADC=80°.
Поделитесь решением
Присоединяйтесь к нам...
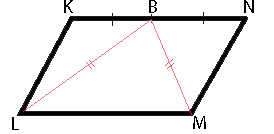В параллелограмме KLMN точка B — середина стороны KN. Известно, что BL=BM. Докажите, что данный параллелограмм — прямоугольник.
В трапеции ABCD AB=CD, ∠BDA=35° и ∠BDC=58°. Найдите угол ABD. Ответ дайте в градусах.
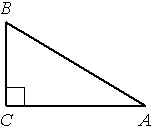В треугольнике ABC угол C прямой, BC=4, sinA=0,8. Найдите AB.
В треугольнике ABC угол C прямой, BC=4, sinA=0,8. Найдите AB.
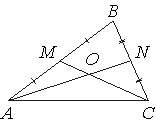Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=21, CM=15. Найдите OM.
Хочу получать новые решения
Ни какого спама
, или 
, где m - средняя линия трапеции. 
Автор: Таська
Комментарии: