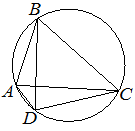
Четырёхугольник ABCD вписан в окружность. Угол ABC равен 70°, угол CAD равен 49°. Найдите угол ABD. Ответ дайте в градусах.
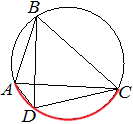∠ABC является вписанным углом и опирается на дугу ADC (красная).
Следовательно, по теореме о вписанном угле, градусная мера дуги ADC равна 70°*2=140°
∠CAD тоже является вписанным углом и опирается на дугу DC.
Следовательно, по теореме о вписанном угле, градусная мера дуги DC равна 49°*2=98°
Тогда легко вычислить градусную меру дуги AD:
140°-98°=42°
Искомый ∠ABD тоже является вписанным углом и опирается на дугу AD.
Следовательно, по теореме о вписанном угле, угол ABD равен:
42°/2=21°
Ответ: 21
Поделитесь решением
Присоединяйтесь к нам...
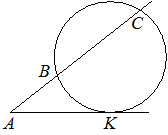Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=8, BC=24. Найдите AK.
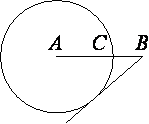На отрезке AB выбрана точка C так, что AC=75 и BC=10. Построена окружность с центром A, проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.
Боковые стороны AB и CD трапеции ABCD равны соответственно 12 и 15, а основание BC равно 3. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
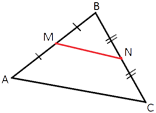Точки M и N являются серединами сторон AB и BC треугольника ABC, AC=24. Найдите MN.
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны
AC втрое больше длины стороны AB. Найдите отношение площади четырехугольника KPCM к площади треугольника ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: