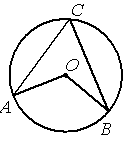
Точка О – центр окружности, /ACB=62° (см. рисунок). Найдите величину угла AOB (в градусах).
По условию /ACB=62°, этот угол является
вписанным углом и равен половине дуги, на которую опирается (
по теореме о вписанном угле).
Следовательно, градусная мера дуги, в нашей задаче, равна 62°*2=124°.
/AOB является
центральным и равен градусной мере дуги, на которую опирается, следовательно, /AOB=124°.
Ответ: /AOB=124°.
Поделитесь решением
Присоединяйтесь к нам...
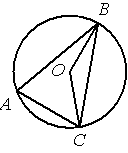Точка О – центр окружности, /BAC=70° (см. рисунок). Найдите величину угла BOC (в градусах).
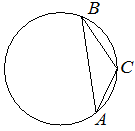В треугольнике ABC угол C равен 120°, AB=22√3. Найдите радиус окружности, описанной около этого треугольника.
Какие из данных утверждений верны? Запишите их номера.
1) У равнобедренного треугольника есть ось симметрии.
2) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.
3) Две окружности пересекаются, если радиус одной окружности больше радиуса другой окружности.
В трапеции ABCD AB=CD, ∠BDA=10° и ∠BDC=109°. Найдите угол ABD. Ответ дайте в градусах.
Сторона равностороннего треугольника равна 14√3. Найдите медиану этого треугольника.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: