
 На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что
∠NBA=47°. Найдите угол NMB. Ответ дайте в градусах.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что
∠NBA=47°. Найдите угол NMB. Ответ дайте в градусах.
Дуга ANB равна дуге AMB, и обе равны 180°, т.к. AB - диаметр.
/NBA является
вписанным в окружность углом, следовательно (по
теореме о вписанном угле) дуга AN равна 47°*2=94°.
Тогда дуга NB равна 180°-94°=86°
/NMB - тоже
вписанный в окружность, следовательно он равен 86°/2=43°
Ответ: 43
Поделитесь решением
Присоединяйтесь к нам...
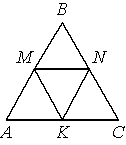 В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равносторонний.
В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равносторонний.
 Две касающиеся внешним образом в точке K окружности, радиусы которых равны 31 и 32, касаются сторон угла с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
Две касающиеся внешним образом в точке K окружности, радиусы которых равны 31 и 32, касаются сторон угла с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
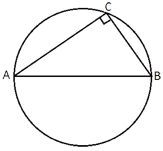 В треугольнике ABC AC=15, BC=5√
В треугольнике ABC AC=15, BC=5√
 В треугольнике ABC угол C равен 90°, BC=2, sinA=0,2. Найдите AB.
В треугольнике ABC угол C равен 90°, BC=2, sinA=0,2. Найдите AB.
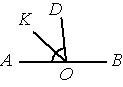 Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB=108°. Ответ дайте в градусах.
Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB=108°. Ответ дайте в градусах.
Комментарии: