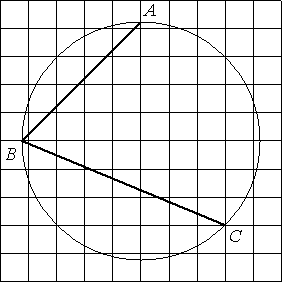
Найдите угол ABC. Ответ дайте в градусах.
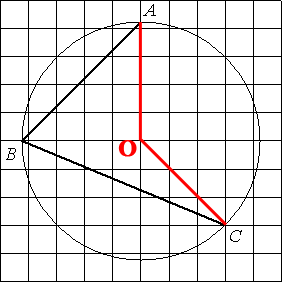Проведем два отрезка от центра окружности к точкам А и С, как показано на рисунке.
По координатной сетке видно, что получившийся угол AOC равен 135° (прямой угол + половина от прямого угла, 90°+45°=135°).
∠AOC является
центральным для окружности, следовательно градусная мера дуги, на которую он опирается, тоже равна 135°.
∠ABC -
вписанный угол и по
теореме равен 135°/2=67,5°
Ответ: 67,5
Поделитесь решением
Присоединяйтесь к нам...
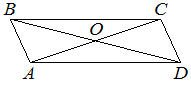Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC=24, BD=28, AB=6. Найдите DO.
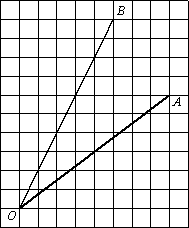Найдите тангенс угла AOB.
Какой угол (в градусах) описывает часовая стрелка за 2 часа 16 минут?
Катеты прямоугольного треугольника равны 20 и 15. Найдите синус наименьшего угла этого треугольника.
В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=79 и BC=BM. Найдите AH.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: