
 ABCDEFGHI – правильный девятиугольник. Найдите угол ADC. Ответ дайте в градусах.
ABCDEFGHI – правильный девятиугольник. Найдите угол ADC. Ответ дайте в градусах.
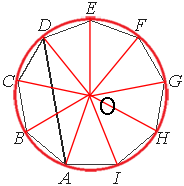 Вокруг любого
правильного многоугольника можно описать окружность, сделаем это.
Вокруг любого
правильного многоугольника можно описать окружность, сделаем это.
Очевидно, что отрезки, проведенные из центра окружности к углам девятиугольника образуют равные углы, так как разбивают девятиугольник на равные треугольники.
Такой угол (например ∠DOE) равен 360°/9=40°
Тогда ∠AOC, который опирается на дугу ABC равен:
∠AOC=40°*2=80°
∠AOC является
центральным, следовательно градусная мера дуги ABC тоже равна 80°
∠ADC тоже опирается на эту же дугу, но является
вписанным, следовательно:
∠ADC=80°/2=40° (по
теореме о вписанном угле)
Ответ: 40
Поделитесь решением
Присоединяйтесь к нам...
 В окружности с центром в точке О проведены диаметры AD и BC, угол
OCD равен 30°. Найдите величину угла OAB.
В окружности с центром в точке О проведены диаметры AD и BC, угол
OCD равен 30°. Найдите величину угла OAB.
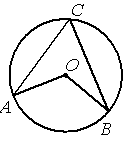 Точка О – центр окружности, /ACB=65° (см. рисунок). Найдите величину угла AOB (в градусах).
Точка О – центр окружности, /ACB=65° (см. рисунок). Найдите величину угла AOB (в градусах).
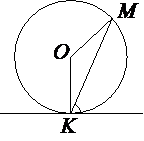 Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 84°. Найдите величину угла OMK. Ответ дайте в градусах.
Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 84°. Найдите величину угла OMK. Ответ дайте в градусах.
 Радиус окружности, описанной около квадрата, равен 16√
Радиус окружности, описанной около квадрата, равен 16√
 Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=9, AC=18, MN=8. Найдите AM.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=9, AC=18, MN=8. Найдите AM.

Комментарии: