Точка О – центр окружности, /ACB=24° (см. рисунок). Найдите величину угла AOB (в градусах).
По условию /ACB=24°, этот угол является
вписанным углом и равен половине дуги, на которую опирается (
по теореме о вписанном угле).
Следовательно, градусная мера дуги, в нашей задаче, равна 24°*2=48°.
/AOB является
центральным и равен градусной мере дуги, на которую опирается, следовательно, /AOB=48°.
Ответ: /AOB=48°.
Поделитесь решением
Присоединяйтесь к нам...
Площадь прямоугольного треугольника равна 2√
Какие из данных утверждений верны? Запишите их номера.
1) Любой параллелограмм можно вписать в окружность.
2) Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны.
3) Точка пересечения двух окружностей равноудалена от центров этих окружностей.
В треугольнике ABC отмечены середины M и N сторон BC и AC соответственно. Площадь треугольника CNM равна 67. Найдите площадь четырёхугольника ABMN.
Медиана BM треугольника ABC равна 3 и является диаметром окружности, пересекающей сторону BC в её середине. Найдите диаметр описанной окружности треугольника ABC.
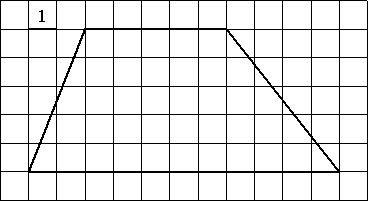Найдите площадь трапеции, изображённой на рисунке.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: