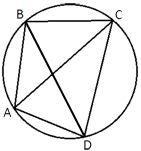Четырехугольник ABCD вписан в окружность. Угол ABC равен 92°, угол CAD равен 60°. Найдите угол ABD. Ответ дайте в градусах.
∠CAD является
вписанным углом и опирается на дугу CD.
∠CBD тоже
вписанный и тоже опирается на ту же дугу CD, следовательно:
∠CAD=∠CBD=60°
∠ABD=∠ABC-∠CBD=92°-60°=32°
Ответ: 32
Поделитесь решением
Присоединяйтесь к нам...
В трапеции ABCD основание AD вдвое больше основания ВС и вдвое больше боковой стороны CD. Угол ADC равен 60°, сторона AB равна 1. Найдите площадь трапеции.
Синус острого угла A треугольника ABC равен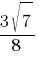 
. Найдите CosA.
Высота BH ромба ABCD делит его сторону AD на отрезки AH=21 и HD=8. Найдите площадь ромба.
В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 55°. Найдите величину угла ODC.
Найдите площадь треугольника, изображённого на рисунке.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2016-12-22 20:34:56) Администратор: Андрей, Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, пишите, обязательно добавим.
(2016-12-22 16:48:54) Андрей: четырехугольник BCDE вписан в окружность.расстояние между точками E и C равно 25, между D и C -7, между D и E -24. найти а) косинус угла CBD; б) BC, если косинус угла BCD=1/5