
 На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что /NBA=11°. Найдите угол NMB. Ответ дайте в градусах.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что /NBA=11°. Найдите угол NMB. Ответ дайте в градусах.
Оговоримся сразу, рисунок несколько не соответствует условию задачи, на рисунке /NBA скорее равен 50°, поэтому не удивляйтесь, что будут расхождения с рисунком.
Угол NBA является
вписанным для данной окружности. Опирается этот угол на дугу AN. градусная мера дуги AN = /NBA*2=11°*2=22° (по
теореме о вписанном угле).
Градусная мера дуги ANB = 180° (т.к. AB - диаметр), следовательно, градусная мера дуги NB = дуга ANB - дуга AN = 180°-22°=158°
/NMB - тоже является
вписанным в окружность и равен половине градусной меры дуги NB (по
теореме).
/NMB=158°/2=79°
Ответ: /NMB=79°
Поделитесь решением
Присоединяйтесь к нам...
 Человек, рост которого равен 1,6 м, стоит на расстоянии 17 м от уличного фонаря. При этом длина тени человека равна 8 м. Определите высоту фонаря (в метрах).
Человек, рост которого равен 1,6 м, стоит на расстоянии 17 м от уличного фонаря. При этом длина тени человека равна 8 м. Определите высоту фонаря (в метрах).
 Проектор полностью освещает экран A высотой 80 см, расположенный на расстоянии 250 см от проектора. На каком наименьшем расстоянии
(в сантиметрах) от проектора нужно расположить экран B высотой 160 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
Проектор полностью освещает экран A высотой 80 см, расположенный на расстоянии 250 см от проектора. На каком наименьшем расстоянии
(в сантиметрах) от проектора нужно расположить экран B высотой 160 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
 В треугольнике ABC известно, что AB=2, BC=3, AC=4. Найдите cos∠ABC.
В треугольнике ABC известно, что AB=2, BC=3, AC=4. Найдите cos∠ABC.
 Окружности радиусов 44 и 77 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
Окружности радиусов 44 и 77 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
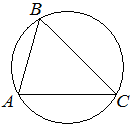 В треугольнике ABC угол C равен 45°, AB=6√
В треугольнике ABC угол C равен 45°, AB=6√

Комментарии: