На окружности отмечены точки A и B так, что меньшая дуга AB равна 66°. Прямая BC касается окружности в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
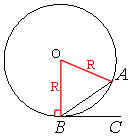Проведем радиусы к точкам A и B, как показано на рисунке.
∠AOB - центральный и опирается на дугу в 66°, следовательно:
∠AOB=66°
Треугольник AOB - равнобедренный, так как две его стороны - это радиусы окружности.
Тогда, по свойству равнобедренного треугольника, углы при основании равны, обозначим их α.
По
теореме о сумме углов треугольника:
∠AOB+∠OAB+∠OBA=180°
66°+α+α=180°
2α=180°-66°=114°
α=114°/2=57°
По
свойству касательной ∠OBC=90°.
∠ABC=∠OBC-∠OBA
∠ABC=90°-57°=33°
Ответ: 33
Поделитесь решением
Присоединяйтесь к нам...
Стороны AC, AB, BC треугольника ABC равны 3√
Проектор полностью освещает экран A высотой 80 см, расположенный на расстоянии 250 см от проектора. На каком наименьшем расстоянии
(в сантиметрах) от проектора нужно расположить экран B высотой 160 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
Прямая, параллельная основаниям трапеции
ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=42, BC=14, CF:DF=4:3.
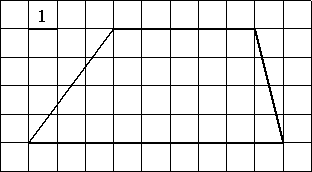Найдите площадь трапеции, изображённой на рисунке.
На окружности отмечены точки A и B так, что меньшая дуга AB равна 26°. Прямая BC касается окружности
в точке B так, что угол ABC острый. Найдите угол ABC. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Дуга, на которую опирается центральный угол имеет ту же градусную меру. 
Автор: Таська
Комментарии: