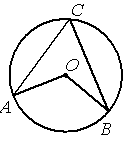
Точка О – центр окружности, /ACB=62° (см. рисунок). Найдите величину угла AOB (в градусах).
По условию /ACB=62°, этот угол является
вписанным углом и равен половине дуги, на которую опирается (
по теореме о вписанном угле).
Следовательно, градусная мера дуги, в нашей задаче, равна 62°*2=124°.
/AOB является
центральным и равен градусной мере дуги, на которую опирается, следовательно, /AOB=124°.
Ответ: /AOB=124°.
Поделитесь решением
Присоединяйтесь к нам...
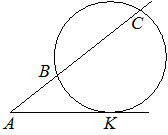Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности
в точке K. Другая прямая пересекает окружность
в точках B и C, причём AB=2, AC=8. Найдите AK.
Точка крепления троса, удерживающего флагшток в вертикальном положении, находится на высоте 8 м от земли. Расстояние от основания флагштока до места крепления троса на земле равно 6 м. Найдите длину троса.
Человек, рост которого равен 1,8 м, стоит на расстоянии 11 м от уличного фонаря. При этом длина тени человека равна 9 м. Определите высоту фонаря (в метрах).
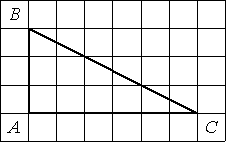Найдите тангенс угла В треугольника ABC, изображённого на рисунке.
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=27, CM=9. Найдите AO.
Хочу получать новые решения
Ни какого спама
Дуга, на которую опирается центральный угол имеет ту же градусную меру. 
Автор: Таська
Комментарии: