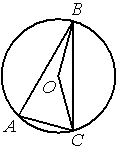
Точка О — центр окружности, ∠BOC=160°. Найдите величину угла BAC (в градусах).
По условию ∠BOC=160°, этот угол является
центральным, соответственно дуга ВC (малая часть) тоже равна 160°.
∠BAC - является
вписанным углом и равен половине дуги, на которую опирается (
по теореме о вписанном угле).
Следовательно, ∠BAC=160°/2=80°.
Ответ: 80
Поделитесь решением
Присоединяйтесь к нам...
Радиус окружности, описанной около квадрата, равен 16√
Радиус вписанной в квадрат окружности равен 4√2. Найдите диагональ этого квадрата.
В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 75°. Найдите величину угла ODC.
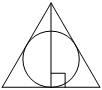Радиус окружности, вписанной в равносторонний треугольник, равен 5. Найдите высоту этого треугольника.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=1:2, KM=23.
Хочу получать новые решения
Ни какого спама
Дуга, на которую опирается центральный угол имеет ту же градусную меру. 
Автор: Таська
Комментарии: