ABCDEFGHI – правильный девятиугольник. Найдите угол ADC. Ответ дайте в градусах.
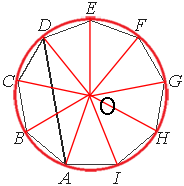Вокруг любого
правильного многоугольника можно описать окружность, сделаем это.
Очевидно, что отрезки, проведенные из центра окружности к углам девятиугольника образуют равные углы, так как разбивают девятиугольник на равные треугольники.
Такой угол (например ∠DOE) равен 360°/9=40°
Тогда ∠AOC, который опирается на дугу ABC равен:
∠AOC=40°*2=80°
∠AOC является
центральным, следовательно градусная мера дуги ABC тоже равна 80°
∠ADC тоже опирается на эту же дугу, но является
вписанным, следовательно:
∠ADC=80°/2=40° (по
теореме о вписанном угле)
Ответ: 40
Поделитесь решением
Присоединяйтесь к нам...
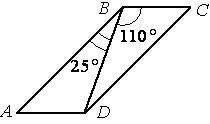Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
25° и 110°. Найдите меньший угол параллелограмма.
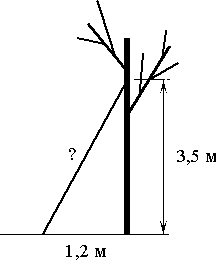Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 3,5 м над землёй, а нижний отстоит от ствола дерева на 1,2 м?
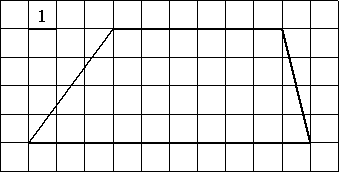Найдите площадь трапеции, изображённой на рисунке.
Укажите номера верных утверждений.
1) Медиана равнобедренного треугольника, проведённая из вершины, противолежащей основанию, перпендикулярна основанию.
2) Диагонали любого прямоугольника делят его на 4 равных треугольника.
3) Для точки, лежащей внутри круга, расстояние до центра круга меньше его радиуса.
Косинус острого угла A треугольника ABC равен 
. Найдите sinA.
Хочу получать новые решения
Ни какого спама
Дуга, на которую опирается центральный угол имеет ту же градусную меру. 
Автор: Таська
Комментарии: