Найдите угол ABC . Ответ дайте в градусах.
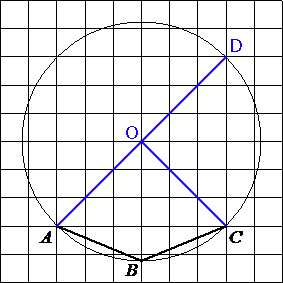Проведем отрезки как показано на рисунке.
∠AOC -
центральный угол.
По рисунку (по клеточкам) видно, что ∠AOC=90°
Следовательно дуга ABC=90°
Тогда дуга ADC=360°-90°=270°
∠ABC опирается на эту дугу ADC и является
вписанным, по
теореме о вписанном угле:
∠ABC=270°/2=135°
Ответ: 135
Поделитесь решением
Присоединяйтесь к нам...
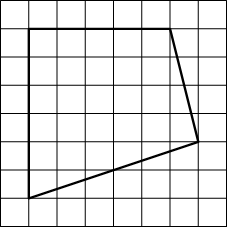Площадь одной клетки равна 1. Найдите площадь фигуры, изображённой на рисунке.
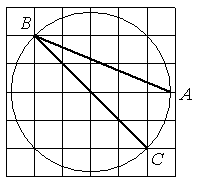Найдите угол ABC. Ответ дайте в градусах.
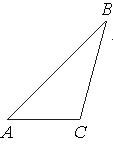В треугольнике ABC угол A равен 45°, угол B равен 30°, BC=8√2. Найдите AC.
Сторона ромба равна 34, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Укажите номера верных утверждений.
1) Если один из углов треугольника прямой, то треугольник прямоугольный.
2) Диагонали квадрата точкой пересечения делятся пополам.
3) Точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к этому отрезку.
Хочу получать новые решения
Ни какого спама
Дуга, на которую опирается центральный угол имеет ту же градусную меру. 
Автор: Таська
Комментарии:
(2015-04-06 22:54:44) Администратор: Елена, тоже вариант...
(2015-04-06 22:20:14) Елена: По сетке чётко видно, что АВС - это часть вписанного в окружность правильного восьмиугольника. Угол АВС - угол правильного восьмиугольника. Он равен 180*(8-2)/8=135