
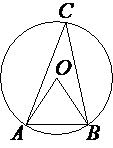 Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 27°.
Треугольник ABC вписан в окружность с центром в точке O. Найдите градусную меру угла C треугольника ABC, если угол AOB равен 27°.
∠AOB является
центральным, следовательно, градусная мера дуги, на которую он опирается, равна этому углу.
∠C является
вписанным, следовательно, его градусная мера вдвое меньше, чем градусная мера дуги, на которую он опирается (по
теореме о вписанной угле).
∠C=27°/2=13,5°
Ответ: ∠C=13,5°
Поделитесь решением
Присоединяйтесь к нам...
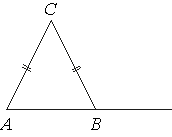 В треугольнике ABC AC=BC. Внешний угол при вершине B равен 121°. Найдите угол C. Ответ дайте в градусах.
В треугольнике ABC AC=BC. Внешний угол при вершине B равен 121°. Найдите угол C. Ответ дайте в градусах.
 В треугольнике ABC угол C равен 90°, sinB=5/8, AB=16. Найдите AC.
В треугольнике ABC угол C равен 90°, sinB=5/8, AB=16. Найдите AC.
Укажите номера верных утверждений.
1) Если угол острый, то смежный с ним угол также является острым.
2) Диагонали квадрата взаимно перпендикулярны.
3) В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности.
Основание AC равнобедренного треугольника ABC равно 12. Окружность радиуса 9 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
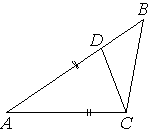 Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=54° и ∠ACB=104°. Найдите угол DCB. Ответ дайте в градусах.
Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=54° и ∠ACB=104°. Найдите угол DCB. Ответ дайте в градусах.
 Дуга, на которую опирается центральный угол имеет ту же градусную меру.
Дуга, на которую опирается центральный угол имеет ту же градусную меру.
Комментарии: