Радиус окружности, вписанной в равнобедренную трапецию, равен 20. Найдите высоту этой трапеции.
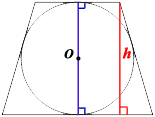Проведем высоту
трапеции (красный отрезок). Высота перпендикулярна обоим основаниям (по определению).
Проведем радиусы окружности к обоим основаниям (синие отрезки).
Очевидно, что радиусы, высота и основания образуют прямоугольник, следовательно, радиусы образуют диаметр, который равен высоте.
h=D=2R=2*20=40.
Ответ: 40
Поделитесь решением
Присоединяйтесь к нам...
Биссектриса CM треугольника ABC делит сторону AB на отрезки AM=12 и MB=18. Касательная к описанной окружности треугольника ABC, проходящая через точку C, пересекает прямую AB в точке D. Найдите CD.
На стороне AC треугольника ABC отмечена точка D так, что AD=3, DC=7. Площадь треугольника ABC равна 20. Найдите площадь треугольника BCD.
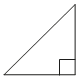В прямоугольном треугольнике гипотенуза равна 82, а один из острых углов равен 45°. Найдите площадь треугольника.
Укажите номера верных утверждений.
1) Медиана равнобедренного треугольника, проведённая из вершины угла, противолежащего основанию, делит этот угол пополам.
2) Не существует прямоугольника, диагонали которого взаимно перпендикулярны.
3) В плоскости для точки, лежащей вне круга, расстояние до центра круга больше его радиуса.
Точки M и N являются серединами сторон AB и BC треугольника ABC соответственно. Отрезки AN
и CM пересекаются в точке O, AN=24, CM=15. Найдите AO.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2021-05-25 11:19:48) рината: найдите площадь изображенной на клетчатой бумаге с размером клетки 2х2 см.