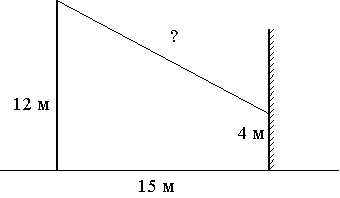
От столба высотой 12 м к дому натянут провод, который крепится на высоте 4 м от земли (см. рисунок). Расстояние от дома до столба 15 м. Вычислите длину провода. Ответ дайте в метрах.
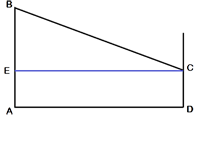Изобразим рисунок схематично. Проведем отрезок СЕ, параллельный AD.
AECD -
прямоугольник, т.к. все углы прямые. Следовательно, СЕ=AD=15 и EA=CD=4.
Треугольник BCE прямоугольный, тогда
по
теореме Пифагора:
BC2=CE2+EB2
BC2=CE2+(BA-EA)2
BC2=152+(12-4)2
BC2=225+64
BC2=289
BC=17.
Ответ: 17
Поделитесь решением
Присоединяйтесь к нам...
В трапеции ABCD AB=CD, ∠BDA=35° и ∠BDC=58°. Найдите угол ABD. Ответ дайте в градусах.
В треугольнике ABC проведена биссектриса AL, угол ALC равен 169°, угол ABC равен 160°. Найдите угол ACB. Ответ дайте в градусах.
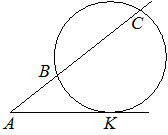Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности
в точке K. Другая прямая пересекает окружность
в точках B и C, причём AB=2, AC=8. Найдите AK.
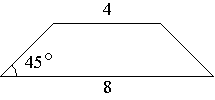В равнобедренной трапеции основания равны 4 и 8, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
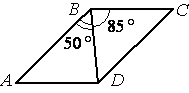Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные
50° и 85°. Найдите меньший угол параллелограмма.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: