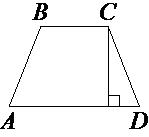ОГЭ, Математика.
Геометрия: Задача №3433A9

Задача №819 из 1087
Условие задачи:

Высота равнобедренной трапеции, проведённая из вершины C, делит основание AD на отрезки длиной 1 и 5. Найдите длину основания BC.

Решение задачи:

Проведем отрезок из точки B перпендикулярно AD, как показано на рисунке.
BCEF - прямоугольник.
Рассмотрим треугольники ABF и DCE.
∠BAF=∠CDE (по второму свойству равнобедренной трапеции).
∠BFA=∠CED=90°
Следовательно, ∠ABF=∠DCE (по теореме о сумме углов треугольника).
AB=CD (по определению равнобедренной трапеции).
Тогда, по второму признаку данные треугольники равны.
Следовательно AF=DE=1.
FE=AE-DE=5-1=4
BC=FE=4 (по свойству прямоугольника).
Ответ: 4

Поделитесь решением

Присоединяйтесь к нам...

Вы можете поблагодарить автора, написать свои претензии или предложения на странице 'Про нас'

Другие задачи из этого раздела

Задача №FC7964

Какие из данных утверждений верны? Запишите их номера.
1) Если при пересечении двух прямых третьей прямой внутренние накрест лежащие углы равны 90°, то эти две прямые параллельны.
2) В любой четырёхугольник можно вписать окружность.
3) Центром окружности, описанной около треугольника, является точка пересечения серединных перпендикуляров к сторонам треугольника.