Точка H является основанием высоты BH, проведенной из вершины прямого угла B прямоугольного треугольника ABC. Окружность с диаметром BH пересекает стороны AB и CB в точках P и K соответственно. Найдите BH, если PK=13.
Вариант №1 (Прислал один из наших пользователей, имя не известно).
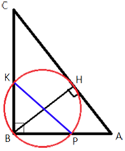∠KBP=90° (по условию)
Прямоугольный треугольник KPB с гипотенузой PK вписан в окружность.
Следовательно, PK является диаметром окружности. (по
теореме об описанной окружности).
KP=BH=13
Ответ: BH=13
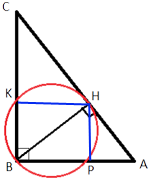Проведем отрезки KH и HP.Поделитесь решением
Присоединяйтесь к нам...
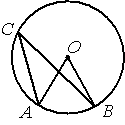Точка О – центр окружности, /AOB=70° (см. рисунок). Найдите величину угла ACB (в градусах).
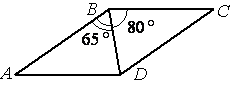Диагональ BD параллелограмма ABCD образует с его сторонами углы, равные 65° и 80°. Найдите меньший угол параллелограмма.
Какие из данных утверждений верны? Запишите их номера.
1) Через точку, не лежащую на данной прямой, можно провести прямую, параллельную этой прямой.
2) Треугольник со сторонами 1, 2, 4 существует.
3) Если в ромбе один из углов равен
90°, то такой ромб — квадрат.
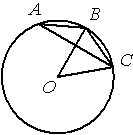Точка О – центр окружности, /BAC=10° (см. рисунок). Найдите величину угла BOC (в градусах).
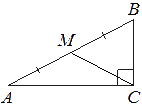В треугольнике ABC угол C равен 90°, M — середина стороны AB, AB=20, BC=10. Найдите CM.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2019-09-05 10:22:32) Администратор: Ольга, не очень понятно, что Вы хотели сказать. Напишите, пожалуйста, поподробней.
(2019-09-04 16:31:29) Ольга: В данной задаче нужно показать два решения на 1 балл и на 0 баллов как в ОГЭ, ПОДЧЕРКНУВ ПОГРЕШНОСТИ ОБОСНОВАТЬ ВЫСТАВЛЕННЫЕ БАЛЛЫ