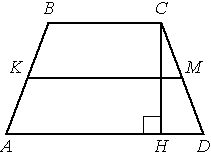
В трапеции АВСD боковые стороны AB и CD равны, СН — высота, проведённая к большему основанию AD. Найдите длину отрезка HD, если средняя линия KM трапеции равна 16, а меньшее основание BC равно 6.
Средняя линия трапеции Lср=(AD+BC)/2
Отсюда AD=2*Lср-BC.
Проведем еще одну высоту из вершины B
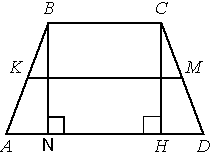и рассмотрим треугольники CDH и ABN.
AB=CD (по условию задачи)
BN=CH, т.к. BCHN -
прямоугольник, образованный параллельными сторонами трапеции и перпендикулярами к ним.
Следовательно, применив
теорему Пифагора, получим, что HD=NA
AD=AN+NH+HD
AD=2*HD+NH, NH=BC (т.к. BCHN - прямоугольник), тогда:
AD=2*HD+BC,
HD=(AD-BC)/2
Ранее мы выяснили, что AD=2*Lср-BC=2*16-6=26, тогда:
HD=(26-6)/2=10.
Ответ: 10
Поделитесь решением
Присоединяйтесь к нам...
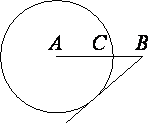На отрезке AB выбрана точка C так, что AC=14 и BC=36. Построена окружность с центром A, проходящая через C. Найдите длину касательной, проведённой из точки B к этой окружности.
Прямая касается окружности в точке K. Точка O – центр окружности. Хорда KM образует с касательной угол, равный 39°. Найдите величину угла OMK. Ответ дайте в градусах.
В треугольнике ABC проведена биссектриса AL, угол ALC равен 112°, угол ABC равен 106°. Найдите угол ACB. Ответ дайте в градусах.
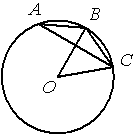Точка О – центр окружности, /BOC=50° (см. рисунок). Найдите величину угла BAC (в градусах).
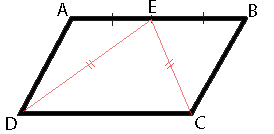В параллелограмме ABCD точка E — середина стороны AB. Известно, что EC=ED. Докажите, что данный параллелограмм - прямоугольник.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2018-01-19 20:09:01) Администратор: Вам что-то не нравится?
(2018-01-19 12:49:04) : это фуфло