
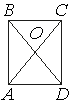
 Диагонали AC и BD прямоугольника ABCD пересекаются
в точке O, BO=37, AB=56. Найдите AC.
Диагонали AC и BD прямоугольника ABCD пересекаются
в точке O, BO=37, AB=56. Найдите AC.
BO=OD (по четвертому свойству прямоугольника).
Тогда:
BD=BO+OD=BO+BO=2*BO=2*37=74
AC=BD=74 (по второму свойству прямоугольника).
Ответ: 74
Поделитесь решением
Присоединяйтесь к нам...
 Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=5, CK=14.
Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=5, CK=14.
 В окружности с центром в точке O проведены диаметры
AD и BC, угол OAB равен 70°. Найдите величину угла OCD.
В окружности с центром в точке O проведены диаметры
AD и BC, угол OAB равен 70°. Найдите величину угла OCD.
 Проектор полностью освещает экран A высотой 50 см, расположенный на расстоянии 140 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 260 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
Проектор полностью освещает экран A высотой 50 см, расположенный на расстоянии 140 см от проектора. На каком наименьшем расстоянии (в сантиметрах) от проектора нужно расположить экран B высотой 260 см, чтобы он был полностью освещён, если настройки проектора остаются неизменными?
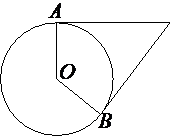 Касательные к окружности с центром O в точках A и B пересекаются под углом 6°. Найдите угол ABO. Ответ дайте в градусах.
Касательные к окружности с центром O в точках A и B пересекаются под углом 6°. Найдите угол ABO. Ответ дайте в градусах.
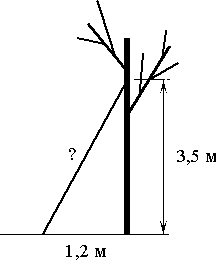 Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 3,5 м над землёй, а нижний отстоит от ствола дерева на 1,2 м?
Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 3,5 м над землёй, а нижний отстоит от ствола дерева на 1,2 м?

Комментарии:
(2021-10-18 13:11:07) Администратор: Никитина Тамара, Я не помогаю решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправьте заявку на добавление задачи, и я ее обязательно добавлю.
(2021-02-23 08:28:10) Никитина Тамара: Диагонали осевого сечения усеченного конуса точкой пересечения делятся в отношении 2:1, считая от большего основания. Угол между диагоналями, обращенный к основаниям конуса, равен 60. Длина диагонали равна 3. Найти объем усеченного конуса.