Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=3, AD=5, AC=24. Найдите AO.
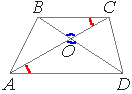Рассмотрим треугольники AOD и BOC.
По определению трапеции, AD||BC, а AC можно рассматривать как секущую при параллельных прямых. Тогда:
∠DAO=∠BCO (накрест лежащие углы).
∠AOD=∠BOC (вертикальные углы).
Тогда, по первому признаку подобия (по двум углам), данные треугольники подобны.
Следовательно, можем записать пропорцию:
AD/BC=AO/OC
5/3=AO/OC
5*OC=3*AO
При этом AO+OC=AC=24
OC=24-AO, подставляем это равенство в ранее полученную пропорцию:
5*(24-AO)=3*AO
120-5*AO=3*AO
120=3*AO+5*AO
120=8*AO
AO=120/8=15
Ответ: 15
Поделитесь решением
Присоединяйтесь к нам...
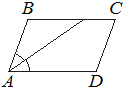Найдите острый угол параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 41°. Ответ дайте в градусах.
Сторона ромба равна 34, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Боковые стороны AB и CD трапеции ABCD равны соответственно 40 и 41, а основание BC равно 16. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
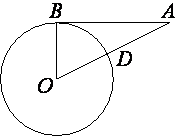Отрезок AB=32 касается окружности радиуса 24 с центром O в точке B. Окружность пересекает отрезок AO в точке D. Найдите AD.
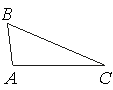В треугольнике ABC известно, что AB=3, BC=8, AC=7. Найдите cos∠ABC.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: