
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ904 –Є–Ј 1087 |
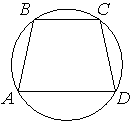 –£–≥–Њ–ї A —В—А–∞–њ–µ—Ж–Є–Є ABCD —Б –Њ—Б–љ–Њ–≤–∞–љ–Є—П–Љ–Є AD –Є BC, –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М, —А–∞–≤–µ–љ 52¬∞. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї B —Н—В–Њ–є —В—А–∞–њ–µ—Ж–Є–Є. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–£–≥–Њ–ї A —В—А–∞–њ–µ—Ж–Є–Є ABCD —Б –Њ—Б–љ–Њ–≤–∞–љ–Є—П–Љ–Є AD –Є BC, –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М, —А–∞–≤–µ–љ 52¬∞. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї B —Н—В–Њ–є —В—А–∞–њ–µ—Ж–Є–Є. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–Я–Њ—Б–Љ–Њ—В—А–Є–Љ –љ–∞ –Њ—Б–љ–Њ–≤–∞–љ–Є—П —В—А–∞–њ–µ—Ж–Є–Є –Ї–∞–Ї –љ–∞ –њ–∞—А–∞–ї–ї–µ–ї—М–љ—Л–µ –њ—А—П–Љ—Л–µ, –∞ –љ–∞ –±–Њ–Ї–Њ–≤—Г—О —Б—В–Њ—А–Њ–љ—Г AB –Ї–∞–Ї –љ–∞ —Б–µ–Ї—Г—Й—Г—О.
–Ґ–Њ–≥–і–∞ —Г–≥–ї—Л A –Є B - –≤–љ—Г—В—А–µ–љ–љ–Є–µ –Њ–і–љ–Њ—Б—В–Њ—А–Њ–љ–љ–Є–µ, —В.–µ.:
∠A+∠B=180¬∞
∠B=180¬∞-∠A
∠B=180¬∞-52¬∞=128¬∞
–Ю—В–≤–µ—В: 128
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
 –Ш–Ј —В–Њ—З–Ї–Є –Р –њ—А–Њ–≤–µ–і–µ–љ—Л –і–≤–µ –Ї–∞—Б–∞—В–µ–ї—М–љ—Л–µ –Ї –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —Б —Ж–µ–љ—В—А–Њ–Љ –≤ —В–Њ—З–Ї–µ –Ю. –Э–∞–є–і–Є—В–µ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —В–Њ—З–Ї–Є –Р –і–Њ —В–Њ—З–Ї–Є –Ю, –µ—Б–ї–Є —Г–≥–Њ–ї –Љ–µ–ґ–і—Г –Ї–∞—Б–∞—В–µ–ї—М–љ—Л–Љ–Є —А–∞–≤–µ–љ 60¬∞, –∞ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —А–∞–≤–µ–љ 8.
–Ш–Ј —В–Њ—З–Ї–Є –Р –њ—А–Њ–≤–µ–і–µ–љ—Л –і–≤–µ –Ї–∞—Б–∞—В–µ–ї—М–љ—Л–µ –Ї –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —Б —Ж–µ–љ—В—А–Њ–Љ –≤ —В–Њ—З–Ї–µ –Ю. –Э–∞–є–і–Є—В–µ —А–∞—Б—Б—В–Њ—П–љ–Є–µ –Њ—В —В–Њ—З–Ї–Є –Р –і–Њ —В–Њ—З–Ї–Є –Ю, –µ—Б–ї–Є —Г–≥–Њ–ї –Љ–µ–ґ–і—Г –Ї–∞—Б–∞—В–µ–ї—М–љ—Л–Љ–Є —А–∞–≤–µ–љ 60¬∞, –∞ —А–∞–і–Є—Г—Б –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —А–∞–≤–µ–љ 8.
–Ь–µ–і–Є–∞–љ–∞ BM —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC —П–≤–ї—П–µ—В—Б—П –і–Є–∞–Љ–µ—В—А–Њ–Љ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є, –њ–µ—А–µ—Б–µ–Ї–∞—О—Й–µ–є —Б—В–Њ—А–Њ–љ—Г BC –≤ –µ—С —Б–µ—А–µ–і–Є–љ–µ. –Э–∞–є–і–Є—В–µ —Н—В–Њ—В –і–Є–∞–Љ–µ—В—А, –µ—Б–ї–Є –і–Є–∞–Љ–µ—В—А –Њ–њ–Є—Б–∞–љ–љ–Њ–є –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC —А–∞–≤–µ–љ 8.
 –Ь–µ–і–Є–∞–љ–∞ BM –Є –±–Є—Б—Б–µ–Ї—В—А–Є—Б–∞ AP —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ K, –і–ї–Є–љ–∞ —Б—В–Њ—А–Њ–љ—Л AC –Њ—В–љ–Њ—Б–Є—В—Б—П –Ї –і–ї–Є–љ–µ —Б—В–Њ—А–Њ–љ—Л AB –Ї–∞–Ї 6:5. –Э–∞–є–і–Є—В–µ –Њ—В–љ–Њ—И–µ–љ–Є–µ –њ–ї–Њ—Й–∞–і–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ AKM –Ї –њ–ї–Њ—Й–∞–і–Є —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–∞ KPCM.
–Ь–µ–і–Є–∞–љ–∞ BM –Є –±–Є—Б—Б–µ–Ї—В—А–Є—Б–∞ AP —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC –њ–µ—А–µ—Б–µ–Ї–∞—О—В—Б—П –≤ —В–Њ—З–Ї–µ K, –і–ї–Є–љ–∞ —Б—В–Њ—А–Њ–љ—Л AC –Њ—В–љ–Њ—Б–Є—В—Б—П –Ї –і–ї–Є–љ–µ —Б—В–Њ—А–Њ–љ—Л AB –Ї–∞–Ї 6:5. –Э–∞–є–і–Є—В–µ –Њ—В–љ–Њ—И–µ–љ–Є–µ –њ–ї–Њ—Й–∞–і–Є —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ AKM –Ї –њ–ї–Њ—Й–∞–і–Є —З–µ—В—Л—А—С—Е—Г–≥–Њ–ї—М–љ–Є–Ї–∞ KPCM.
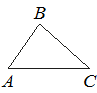 –Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC –Є–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ AB=5, BC=7, AC=9. –Э–∞–є–і–Є—В–µ cos∠ABC.
–Т —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABC –Є–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ AB=5, BC=7, AC=9. –Э–∞–є–і–Є—В–µ cos∠ABC.
 –Я–ї–Њ—Й–∞–і—М –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ–∞ 2450√
–Я–ї–Њ—Й–∞–і—М –њ—А—П–Љ–Њ—Г–≥–Њ–ї—М–љ–Њ–≥–Њ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞–≤–љ–∞ 2450√

–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є:
(2021-11-29 13:08:07) –Р—А–Є–љ–∞: –Я–Њ—В
(2020-03-31 21:13:59) –Р–і–Љ–Є–љ–Є—Б—В—А–∞—В–Њ—А: –Т–Є—В–∞–ї–Є–Ї, –Ь—Л –љ–µ –њ–Њ–Љ–Њ–≥–∞–µ–Љ —А–µ—И–Є—В—М –і–Њ–Љ–∞—И–љ–µ–µ –Ј–∞–і–∞–љ–Є–µ, —Ж–µ–ї—М —Б–∞–є—В–∞ - –њ–Њ–і—А–Њ–±–љ–Њ —А–∞–Ј–Њ–±—А–∞—В—М –Ј–∞–і–∞—З–Є, –Ї–Њ—В–Њ—А—Л–µ –±—Г–і—Г—В –љ–∞ —Н–Ї–Ј–∞–Љ–µ–љ–∞—Е, —З—В–Њ–±—Л —Г—З–∞—Й–Є–µ—Б—П –љ–∞—Г—З–Є–ї–Є—Б—М –Є—Е —А–µ—И–∞—В—М —Б–∞–Љ–Њ—Б—В–Њ—П—В–µ–ї—М–љ–Њ. –Х—Б–ї–Є –љ–∞–є–і–µ—В–µ –њ–Њ—Е–Њ–ґ—Г—О –Ј–∞–і–∞—З—Г –љ–∞ —Б–∞–є—В–µ fipi.ru, –Њ—В–њ—А–∞–≤—М—В–µ –Ј–∞—П–≤–Ї—Г –љ–∞ –і–Њ–±–∞–≤–ї–µ–љ–Є–µ –Ј–∞–і–∞—З–Є, –Є –Љ—Л –µ–µ –Њ–±—П–Ј–∞—В–µ–ї—М–љ–Њ –і–Њ–±–∞–≤–Є–Љ.
(2020-03-18 17:40:14) –Т–Є—В–∞–ї–Є–Ї: –£–≥–Њ–ї A —В—А–∞–њ–µ—Ж–Є–Є ABCD —Б –Њ—Б–љ–Њ–≤–∞–љ–Є—П–Љ–Є AD –Є BC, –≤–њ–Є—Б–∞–љ–љ–Њ–є –≤ –Њ–Ї—А—Г–ґ–љ–Њ—Б—В—М, —А–∞–≤–µ–љ 73¬∞. –Э–∞–є–і–Є—В–µ —Г–≥–Њ–ї C —Н—В–Њ–є —В—А–∞–њ–µ—Ж–Є–Є. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.