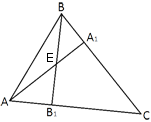Высоты AA1 и BB1 остроугольного треугольника ABC пересекаются в точке E. Докажите, что углы AA1B1 и ABB1 равны.
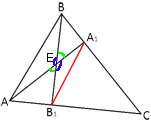Проведем отрезок A1B1 и рассмотрим треугольники EB1A и EA1B.
∠A1EB=∠B1EA (так как они
вертикальные).
∠EB1A=∠EA1B=90° (так как BB1 и AA1 -
высоты).
По
первому признаку подобия треугольников, рассматриваемые треугольники
подобны.
Следовательно:
EB1/EA1=EA/EB
Рассмотрим треугольники EA1B1 и EAB
∠BEA=∠B1EA1 (так как они
вертикальные).
Как мы выяснили ранее:
EB1/EA1=EA/EB
Умножим левую и правую части равенства на EA1, получим:
EB1=EA1*EA/EB
Разделим левую и правую части на EA, получаем:
EB1/EA=EA1/EB
Получается, что по
второму признаку подобия треугольников, треугольники EA1B1 и EAB
подобны.
Следовательно, по
определению, углы AA1B1 и ABB1 равны.
Поделитесь решением
Присоединяйтесь к нам...
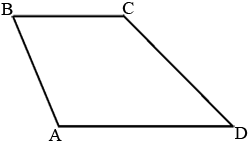Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=32.
Укажите номера верных утверждений.
1) Медиана равнобедренного треугольника, проведённая из вершины угла, противолежащего основанию, делит этот угол пополам.
2) Не существует прямоугольника, диагонали которого взаимно перпендикулярны.
3) В плоскости для точки, лежащей вне круга, расстояние до центра круга больше его радиуса.
Найдите площадь трапеции, диагонали которой равны 13 и 11, а средняя линия равна 10.
Основания трапеции равны 3 и 9, а высота равна 5. Найдите среднюю линию этой трапеции.
Окружности радиусов 25 и 100 касаются внешним образом. Точки A и B лежат на первой окружности, точки C и D — на второй. При этом AC и BD — общие касательные окружностей. Найдите расстояние между прямыми AB и CD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-05-10 22:22:34) Администратор: Дмитрий, если не сложно, то пришлите, пожалуйста, Ваш вариант решения на admin@otvet-gotov.ru
(2017-05-08 09:36:21) Дмитрий: С помощью описанной окружности решение короче и легче