
 В треугольнике ABC проведена биссектриса AL, угол ALC равен 52°, угол ABC равен 13°. Найдите угол ACB. Ответ дайте в градусах.
В треугольнике ABC проведена биссектриса AL, угол ALC равен 52°, угол ABC равен 13°. Найдите угол ACB. Ответ дайте в градусах.
Рассмотрим треугольник ABL.
∠BLA=180°-∠ALC=180°-52°=128° (т.к. это
смежные углы)
По
теореме о сумме углов треугольника:
180°=∠ABC+∠BLA+∠LAB=13°+128°+∠LAB
∠LAB=180°-13°-128°=39°
Рассмотрим треугольник ALC.
∠LAC=∠LAB=39° (т.к. AL -
биссектриса)
По
теореме о сумме углов треугольника:
180°=∠ALC+∠ACB+∠LAC=52°+∠ACB+39°
∠ACB=180°-52°-39°=89°
Ответ: 89
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC AC=35, BC=5√
В треугольнике ABC AC=35, BC=5√
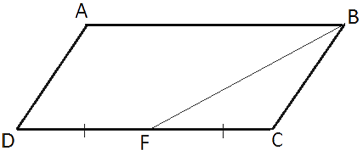 Сторона CD параллелограмма ABCD вдвое больше стороны BC. Точка F — середина стороны CD. Докажите, что BF — биссектриса угла ABC.
Сторона CD параллелограмма ABCD вдвое больше стороны BC. Точка F — середина стороны CD. Докажите, что BF — биссектриса угла ABC.
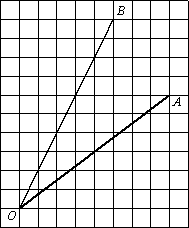 Найдите тангенс угла AOB.
Найдите тангенс угла AOB.
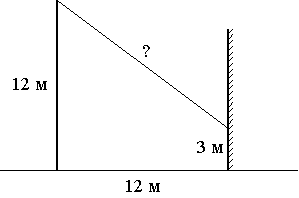 От столба высотой 12 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 12 м. Вычислите длину провода.
От столба высотой 12 м к дому натянут провод, который крепится на высоте 3 м от земли (см. рисунок). Расстояние от дома до столба 12 м. Вычислите длину провода.
 ABCDEFGHI – правильный девятиугольник. Найдите угол ADC. Ответ дайте в градусах.
ABCDEFGHI – правильный девятиугольник. Найдите угол ADC. Ответ дайте в градусах.

Комментарии: