
 Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=71° и ∠OAB=39°. Найдите угол BCO. Ответ дайте в градусах.
Точка O – центр окружности, на которой лежат точки A, B и C. Известно, что ∠ABC=71° и ∠OAB=39°. Найдите угол BCO. Ответ дайте в градусах.
Вариант №1 Предложила пользователь Надя.
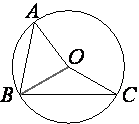 Проведем отрезок OB.
Проведем отрезок OB.
Рассмотрим треугольник AOB.
Так как AO=BO (это радиусы окружности), то данный треугольник
равнобедренный.
Следовательно, ∠OAB=∠ABO=39° (по
свойству равнобедренного треугольника)
∠OBC=∠ABC-∠ABO=71°-39°=32°.
Треугольник BOC тоже
равнобедренный, т.к. OB=OC (радиусы окружности).
Следовательно, ∠OBC=∠BCO=32° (по
свойству равнобедренного треугольника).
Ответ: 32
 Продолжим отрезок AO до отрезка BC, пересечение обозначим буквой E (как показано на рисунке).
Продолжим отрезок AO до отрезка BC, пересечение обозначим буквой E (как показано на рисунке).Поделитесь решением
Присоединяйтесь к нам...
 Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=2:3, KM=14.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=2:3, KM=14.
 Основания равнобедренной трапеции равны 16 и 96, боковая сторона равна 58. Найдите длину диагонали трапеции.
Основания равнобедренной трапеции равны 16 и 96, боковая сторона равна 58. Найдите длину диагонали трапеции.
 Высота BH ромба ABCD делит его сторону AD на отрезки AH=21 и HD=8. Найдите площадь ромба.
Высота BH ромба ABCD делит его сторону AD на отрезки AH=21 и HD=8. Найдите площадь ромба.
 Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 6.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 6.
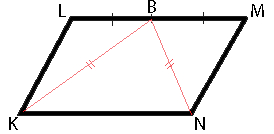 В параллелограмме KLMN точка B — середина стороны LM. Известно, что BK=BN. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме KLMN точка B — середина стороны LM. Известно, что BK=BN. Докажите, что данный параллелограмм — прямоугольник.

Комментарии: