Укажите номера верных утверждений.
1) Если угол острый, то смежный с ним угол также является острым.
2) Диагонали квадрата взаимно перпендикулярны.
3) В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности.
Рассмотрим каждое утверждение:
1) "Если угол острый, то смежный с ним угол также является острым". Сумма
смежных углов равна 180°, следовательно, один из
смежных углов острый (<90°), то другой тупой (>90°). Т.е. это утверждение неверно.
2) "Диагонали квадрата взаимно перпендикулярны", это утверждение верно (по
свойству квадрата).
3) "В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности", это утверждение верно (по
определению окружности).
Поделитесь решением
Присоединяйтесь к нам...
Стороны AC, AB, BC треугольника ABC равны 2√
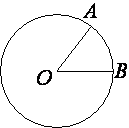На окружности с центром в точке O отмечены точки A и B так, что ∠AOB=66°. Длина меньшей дуги AB равна 99. Найдите длину большей дуги AB.
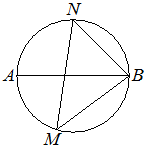На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что ∠NBA=41°. Найдите угол NMB. Ответ дайте в градусах.
В трапеции ABCD боковая сторона AB перпендикулярна основанию BC. Окружность проходит через точки C и D и касается прямой AB в точке E. Найдите расстояние от точки E до прямой CD, если AD=14, BC=12.
В треугольнике ABC с тупым углом ABC проведены высоты AA1 и CC1. Докажите, что треугольники A1BC1 и ABC подобны.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2016-01-16 21:32:52) Администратор: Владимир, на нашем сайте пока нет единой базы со всеми определениями, теоремами и т.д. На сайд добавляются только те материалы, которые использовались при решении задач. Второе, в свойствах биссектрисы есть теорема о сторонах.
(2016-01-16 17:26:11) Владимир: Большое спасибо за сайт. Замечательный сайт. Очень помогает. Но вот ищу свойства высоты, и никак. Наподобие свойств медианы, бисектрисы. И второе. В свойствах бисектрисы не нашел то что она делит противоположную сторону на отрезки пропорциональные остальным двум сторонам. Или это не свойство? Тогдп что это?