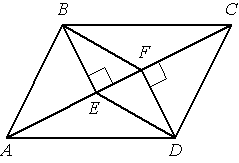
В параллелограмме АВСD проведены перпендикуляры ВЕ и DF к диагонали АС (см. рисунок). Докажите, что отрезки ВF и DЕ параллельны.
1) Рассмотрим треугольники ABE и CDF.
AB=CD (по
свойству параллелограмма).
/BAE=/DCF (т.к. это
внутренние накрест-лежащие углы для параллельных BC и AD и секущей AC).
/BEA=/DFC (т.к. оба эти угла прямые по условию).
Если два угла у данных треугольников попарно равны, то и третьи углы равны (по
теореме о сумме углов треугольника).
Следовательно треугольники ABE и CDF равны (по
второму признаку равенства треугольников). Отсюда следует, что BE=FD
2) Рассмотрим треугольники BFE и DEF.
BE=FD (из пункта 1), EF-общая сторона, /BEF=/DFE (т.к. это прямые углы по условию).
Следовательно треугольники BFE и DEF равны (по
первому признаку равенства треугольников). Отсюда следует, что BF=ED.
3) В итоге получаем, BF=ED и BE=FD, следовательно ВFDЕ —
параллелограмм (по
свойству параллелограмма).
Следовательно, ВF и DЕ параллельны (по
определению).
Поделитесь решением
Присоединяйтесь к нам...
Площадь прямоугольного треугольника равна 392√
В треугольнике ABC известно, что AB=6, BC=12, sin∠ABC=1/4. Найдите площадь треугольника ABC.
Найдите больший угол равнобедренной трапеции ABCD, если диагональ АС образует с основанием AD и боковой стороной АВ углы, равные 30° и 45° соответственно. Ответ дайте в градусах.
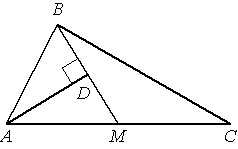Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит её пополам. Найдите сторону АВ, если сторона АС равна 10.
В равнобедренной трапеции основания равны 2 и 8, а один из углов между боковой стороной и основанием равен
45°. Найдите площадь трапеции.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: