
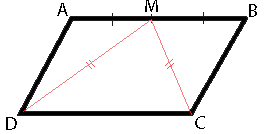
 В параллелограмме ABCD точка M — середина стороны AB. Известно, что MC=MD. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме ABCD точка M — середина стороны AB. Известно, что MC=MD. Докажите, что данный параллелограмм — прямоугольник.
Рассмотрим треугольники DAM и MBC. AM=MB, т.к. точка M - середина AB, MC=MD (из условия задачи), AD=BC (по свойству параллелограмма). Соответственно, треугольники DAM и MBC равны (по третьему признаку равенства треугольников).
Из равенства этих треугольников следует, что /DAM=/MBC.
AD||BC (по определению параллелограмма), рассмотрим сторону AB как секущую к этим параллельным сторонам. Тогда получается, что сумма углов DAM и MBC равна 180°, т.к. эти углы являются внутренними односторонними. Отсюда следует, что каждый из этих углов равен 90°.
Теперь рассмотрим стороны AB и CD, они параллельны (тоже по определению параллелограмма). Рассмотрим сторону AD как секущую к этим параллельным сторонам.
/DAM и /ADC - внутренние односторонние. Следовательно их сумма равна 180°. А так как /DAM=90°, то /ADC тоже равен 90°.
Аналогично доказывается, что /BCD тоже равен 90°.
Параллелограмм, у которого все углы прямые (т.е. 90°) называется прямоугольником (по определению).
Поделитесь решением
Присоединяйтесь к нам...
Синус острого угла A треугольника ABC равен 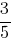 . Найдите CosA.
. Найдите CosA.
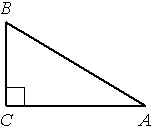 В треугольнике ABC угол C прямой, BC=4, sinA=0,8. Найдите AB.
В треугольнике ABC угол C прямой, BC=4, sinA=0,8. Найдите AB.
Какие из данных утверждений верны? Запишите их номера.
1) Против большей стороны треугольника лежит меньший угол.
2) Любой квадрат можно вписать в окружность.
3) Площадь трапеции равна произведению средней линии на высоту.
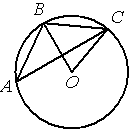 Точка О – центр окружности, /BAC=20° (см. рисунок). Найдите величину угла BOC (в градусах).
Точка О – центр окружности, /BAC=20° (см. рисунок). Найдите величину угла BOC (в градусах).
 Катеты прямоугольного треугольника равны 5√
Катеты прямоугольного треугольника равны 5√

Комментарии: