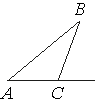
В треугольнике ABC угол C равен 133°. Найдите внешний угол при вершине C. Ответ дайте в градусах.
Внутренний угол С треугольника ABC и внешний угол при вершине C называются
смежными.
Т.е. их сумма равна 180°.
Тогда, внешний угол при вершине C равен 180°-133°=47°
Ответ: 47
Поделитесь решением
Присоединяйтесь к нам...
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=24, AC=21, MN=14. Найдите AM.
Площадь равнобедренного треугольника равна 144√
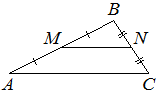Точки M и N являются серединами сторон AB и BC треугольника ABC, сторона AB равна 28, сторона BC равна 19, сторона AC равна 34. Найдите MN.
На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,6 м, если длина его тени равна 2 м, высота фонаря 4 м?
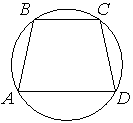Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 32°. Найдите угол C этой трапеции. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2021-10-20 17:13:15) Администратор: Витя, Я не помогаю решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправьте заявку на добавление задачи, и я ее обязательно добавлю.
(2021-02-17 10:55:13) витя: В Δ АВС угол В = 44º, а внешний угол при вершине А равен 100º. Найти угол ВСА.
(2021-02-17 10:54:20) витя: 1 В треугольнике два угла равны 39° и 54°. Найдите его третий угол. 2 В треугольнике ABC известно, что AB=BC, угол B = 116°. Найдите остальные углы. 3 В Δ АВС угол В = 44º, а внешний угол при вершине А равен 100º. Найти угол ВСА. 4 В прямоугольном треугольнике один из острых углов равен 61º. Найти градусную меру внешнего угла при вершине другого острого угла. 5 В Δ АВС угол А = 36º, угол С = 49º. Сравните отрезки АС и ВС. Определите вид треугольника.