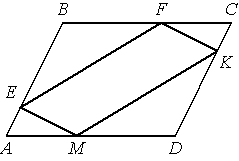
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, СF = АM. Докажите, что EFKM — параллелограмм.
1) Рассмотрим треугольники АЕМ и CKF.
АЕ=CK (по условию задачи)
/A=/C (по
свойству параллелограмма)
СF=АM (по условию задачи).
Следовательно, треугольники АЕМ и CKF равны (по первому признаку).
Поэтому ЕМ=FK.
2) Рассмотрим треугольники EBF и KDM.
Т.к. AB=CD и AD=BC (по
свойству параллелограмма), а АЕ = CK и СF = АM (по условию задачи), то BE=KD и BF=DM.
/B=/D (по
свойству параллелограмма).
Следовательно, треугольники EBF и KDM (по первому признаку). А это значит, что EF=KM.
Из пунктов 1 и 2 (равенство сторон) следует, что EFKM —
параллелограмм (по
свойству параллелограмма).
Поделитесь решением
Присоединяйтесь к нам...
Какие из данных утверждений верны? Запишите их номера.
1) Через две различные точки на плоскости проходит единственная прямая.
2) В любом прямоугольнике диагонали взаимно перпендикулярны.
3) У равностороннего треугольника три оси симметрии.
К окружности с центром в точке O проведены касательная AB и секущая AO. Найдите радиус окружности, если AB=21, AO=75.
Найдите угол ABC . Ответ дайте в градусах.
Найдите площадь трапеции, изображённой на рисунке.
Периметр треугольника равен 48, одна из сторон равна 18,
а радиус вписанной в него окружности равен 3. Найдите площадь этого треугольника.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: