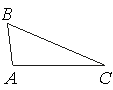
В треугольнике ABC известно, что AB=3, BC=8, AC=7. Найдите cos∠ABC.
По
теореме косинусов:
AC2=AB2+BC2-2*AB*BC*cos∠ABC
72=32+82-2*3*8*cos∠ABC
49=9+64-48*cos∠ABC
49-9-64=-48*cos∠ABC
-24=-48*cos∠ABC |:(-24)
1=2*cos∠ABC
cos∠ABC=1/2=0,5
Ответ: 0,5
Поделитесь решением
Присоединяйтесь к нам...
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=20, DK=15, BC=12. Найдите AD.
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 8, тангенс угла BAC равен 4/3. Найдите радиус вписанной окружности треугольника ABC.
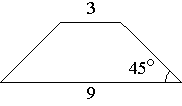В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
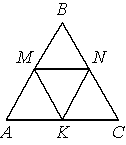В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что ВMKN — ромб.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: