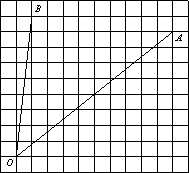
Найдите тангенс угла
AOB.
Вариант №1 (Прислал пользователь Евгений)
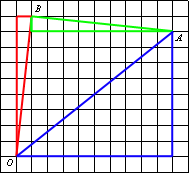Проведем отрезок AB.
Найдем каждую сторону треугольника ABO по
теореме Пифагора:
AO2=102+82
AO2=100+64=164
AO=√
AB2=92+12
AB2=81+1=82
AB=√
BO2=92+12
BO2=81+1=82
BO=√
По
теореме косинусов:
AB2=AO2+BO2-2AO*BO*cos∠AOB
(√
82=164+82-2√
-164=-2√
82=√
82=2√
41=√
cos∠AOB=41/√
По основной тригонометрической формуле:
sin2∠AOB+cos2∠AOB=1
sin2∠AOB+(1/√
sin2∠AOB+1/2=1
sin2∠AOB=1/2
sin∠AOB=1/√
tg∠AOB=sin∠AOB/cos∠AOB=(1/√
Ответ: tg∠AOB=1
Достроим чертеж до двух
прямоугольных треугольников. Найдем
тангенсы для обоих треугольников для их углов О.Поделитесь решением
Присоединяйтесь к нам...
Центральный угол AOB, равный
60°, опирается на хорду АВ длиной 4. Найдите радиус окружности.
Какие из данных утверждений верны? Запишите их номера.
1) На плоскости существует единственная точка, равноудалённая от концов отрезка.
2) В любой треугольник можно вписать окружность.
3) Если в параллелограмме две смежные стороны равны, то такой параллелограмм является ромбом.
Какое из следующих утверждений верно?
1) Площадь квадрата равна произведению двух его смежных сторон.
2) Диагональ трапеции делит её на два равных треугольника.
3) Если две стороны одного треугольника соответственно равны двум сторонам другого треугольника, то такие треугольники равны.
Четырёхугольник ABCD вписан в окружность. Прямые AB и CD пересекаются в точке K, BK=20, DK=15, BC=12. Найдите AD.
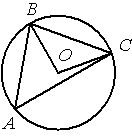Точка О – центр окружности, /BOC=100° (см. рисунок). Найдите величину угла BAC (в градусах).
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: