
 В треугольнике ABC известно, что AB=2, BC=3, AC=4. Найдите cos∠ABC.
В треугольнике ABC известно, что AB=2, BC=3, AC=4. Найдите cos∠ABC.
По
теореме косинусов:
AC2=AB2+BC2-2*AB*BC*cos∠ABC
42=22+32-2*2*3*cos∠ABC
16=4+9-12cos∠ABC
16-4-9=-12cos∠ABC
3=-12cos∠ABC
cos∠ABC=3/(-12)=-1/4=-0,25
Ответ: -0,25
Поделитесь решением
Присоединяйтесь к нам...
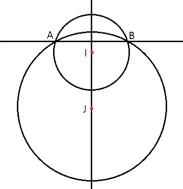 Окружности с центрами в точках I и J пересекаются в точках A и B, причём точки I и J лежат по одну сторону от прямой AB. Докажите, что AB⊥IJ.
Окружности с центрами в точках I и J пересекаются в точках A и B, причём точки I и J лежат по одну сторону от прямой AB. Докажите, что AB⊥IJ.
 Найдите площадь трапеции, диагонали которой равны 13 и 11, а средняя линия равна 10.
Найдите площадь трапеции, диагонали которой равны 13 и 11, а средняя линия равна 10.
 В трапеции ABCD AD=4, BC=1, а её площадь равна 35. Найдите площадь треугольника ABC.
В трапеции ABCD AD=4, BC=1, а её площадь равна 35. Найдите площадь треугольника ABC.
Катеты прямоугольного треугольника равны
√
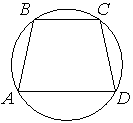 Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 32°. Найдите угол C этой трапеции. Ответ дайте в градусах.
Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 32°. Найдите угол C этой трапеции. Ответ дайте в градусах.

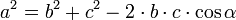
Комментарии: