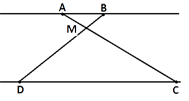Отрезки AB и DC лежат на параллельных прямых, а отрезки AC и BD пересекаются в точке M. Найдите MC, если AB=12, DC=48, AC=35.
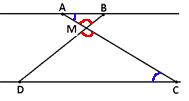Рассмотрим треугольники ABM и CDM.
∠AMB=∠CMD (так как они
вертикальные).
∠BAM=∠MCD (так как они
внутренние накрест-лежащие).
Следовательно, по
первому признаку подобия треугольников, данные треугольники
подобны.
Тогда, мы можем записать:
DC/AB=MC/AM
48/12=MC/AM
4=MC/AM
4=MC/AM
MC=4AM
AC=AM+MC (по рисунку)
35=AM+4AM
35=5AM
AM=7
MC=4AM=4*7=28
ответ: MC=28
Поделитесь решением
Присоединяйтесь к нам...
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите AC, если диаметр окружности равен 7.5, а AB=2.
Укажите номера верных утверждений.
1) Если один из углов треугольника прямой, то треугольник прямоугольный.
2) Диагонали квадрата точкой пересечения делятся пополам.
3) Точка, равноудалённая от концов отрезка, лежит на серединном перпендикуляре к этому отрезку.
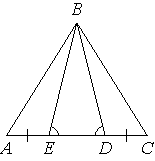На стороне АС треугольника АВС выбраны точки D и E так, что углы АDB и BEC равны (см. рисунок). Оказалось, что отрезки AЕ и CD тоже равны. Докажите, что треугольник АВС — равнобедренный.
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB=9, AC=18, MN=8. Найдите AM.
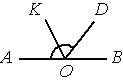Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB=52°. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2017-01-23 20:14:14) Администратор: Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, пишите, обязательно добавим.
(2017-01-23 08:25:28) : 3Х^3+5х^2-х-5=0
(2017-01-23 08:24:49) : 3Х^3+5х^2-х-5=0