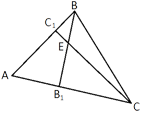Высоты BB1 и CC1 остроугольного треугольника ABC пересекаются в точке E. Докажите, что углы BB1C1 и BCC1 равны.
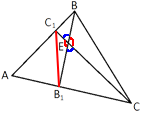Проведем отрезок B1C1 и рассмотрим треугольники EB1C и EC1B.
∠C1EB=∠B1EC (так как они
вертикальные).
∠EB1C=∠EC1B=90° (так как BB1 и CC1 -
высоты).
По
первому признаку подобия треугольников, рассматриваемые треугольники
подобны.
Следовательно:
EB1/EC1=EC/EB
Рассмотрим треугольники EС1B1 и ECB
∠BEC=∠B1EC1 (так как они
вертикальные).
Как мы выяснили ранее:
EB1/EC1=EC/EB
Умножим левую и правую части равенства на EC1, получим:
EB1=EC1*EC/EB
Разделим левую и правую части на EC, получаем:
EB1/EC=EC1/EB
Получается, что по
второму признаку подобия треугольников, треугольники EС1B1 и ECB
подобны.
Следовательно, по
определению, углы BB1C1 и BCC1 равны.
Поделитесь решением
Присоединяйтесь к нам...
Углы при одном из оснований трапеции равны 48° и 42°, а отрезки, соединяющие середины противоположных сторон трапеции равны 6 и 3. Найдите основания трапеции.
Катеты прямоугольного треугольника равны √
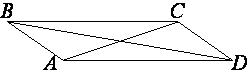В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=169°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
Укажите номера верных утверждений.
1) Если угол острый, то смежный с ним угол также является острым.
2) Диагонали квадрата взаимно перпендикулярны.
3) В плоскости все точки, равноудалённые от заданной точки, лежат на одной окружности.
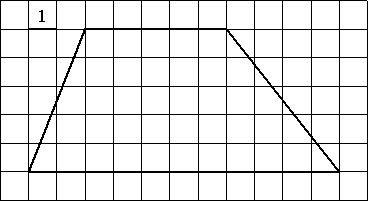Найдите площадь трапеции, изображённой на рисунке.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: